题目内容
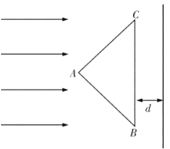
【题目】如图,某种透明材料做成的三棱镜ABC,其截面为等腰直角三角形,已知BC的边长为a,现用一束宽度为a的单色平行光束,以垂直于BC面的方向正好入射到该三棱镜的AB、AC面上,结果所有从AB、AC面入射的光线进入后全部直接到达BC面。某同学用遮光板挡住AC,发现光从BD间射出(D未在BC边标出),已知该材料对此平行光束的折射率![]() 。
。
①求单色平行光束到达BC边的范围BD的长度;
②拿掉遮光板,这些直接到达BC面的光线从BC面折射而出后,如果照射到一块平行于BC的屏上形成光斑,则当屏到BC面的距离d满足什么条件时,此光斑分不成两部分?(结果可以保留根式)
【答案】①![]() ②
②![]()
【解析】
光路如图所示:
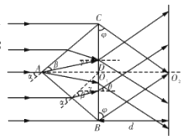
①由题意可知,遮光板挡住AC,单色平行光東经AB面折射后射到BC之间的BD这些光线在三棱镜中是平行的,设光线进入AB面时的入射角为![]() 和折射角为
和折射角为![]() ,由几何关系可得:
,由几何关系可得:
![]() =
=![]()
折射率![]() ,得
,得
![]()
即
![]()
由几何关系有
![]()
②如图O1为BC的中点,从BC射出的光线与AO1的延长线交于O2,根据对称性光斑分不成两部分。由几何关系有:
![]()
![]()
得
![]()
则有
![]()
![]()

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目