��Ŀ����
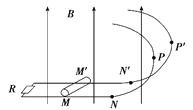
����Ŀ����ͼ��ʾ���⻬��ƽ�еĽ��������ˮƽ��(��˽�����ֵΪR�Ķ�ֵ����)�Ͱ�Բ���������֣����ι��������N��N���㣬Բ���İ뾶Ϊr�������������Ŀ���Ϊd������������ڴŸ�Ӧǿ��ΪB��������ֱ���ϵ���ǿ�ų��У�����Ϊm����Ϊd������ΪR�Ľ���ϸ�����ڿ���ϵ�MM������MN��r.��t��0ʱ�̣�������ϸ��һ����ֱ����ϸ�ˡ�ˮƽ���ҵij��ٶ�v0��֮�����ϸ���ع���˶�����t��t1ʱ�̣�����ϸ�����ٶ�vͨ����Բ�ĵȸߵ�P��P������t��t2ʱ�̣�����ϸ��ǡ��ͨ��Բ���������ߵ㣬����ϸ������ʼ�սӴ����ã�����ĵ���Ϳ������������ƣ��������ٶ�Ϊg.����˵����ȷ����(����)
A. t��0ʱ�̣�����ϸ�����˵ĵ�ѹΪBdv0
B. t��t1ʱ�̣�����ϸ�����ܵİ�����Ϊ![]()
C. ��t��0��t��t1ʱ�̣�ͨ������ϸ�˺����ĵ���Ϊ![]()
D. ��t��0��t��t2ʱ�̣���ֵ����R�����Ľ�����Ϊ![]()
���𰸡�CD
��������A�� t��0ʱ�̣�����ϸ�˲����ĸ�Ӧ�綯��![]() ������ϸ�����˵ĵ�ѹ
������ϸ�����˵ĵ�ѹ![]() ����A�����
����A�����
B��t��t1ʱ�̣�����ϸ�˵��ٶ���ų�ƽ�У����и�Ÿ��ߣ���������Ӧ���������Դ�ʱ������ϸ�˲��ܰ���������B�����
C����t��0��t��t1ʱ�̣���·�е�ƽ���綯��![]() ����·�еĵ���
����·�еĵ���![]() �������ʱ����ͨ������ϸ�˺����ĵ���
�������ʱ����ͨ������ϸ�˺����ĵ���![]() ����ã�
����ã� ![]() ����C����ȷ��
����C����ȷ��
D�����ͨ����ߵ��ٶ�Ϊ![]() ������ϸ��ǡ��ͨ��Բ���������ߵ㣬�Ը�������������ţ�ٵڶ����ɿɵã�
������ϸ��ǡ��ͨ��Բ���������ߵ㣬�Ը�������������ţ�ٵڶ����ɿɵã� ![]() �����
�����![]()
��t��0��t��t2ʱ�̣��ݹ��ܹ�ϵ�ɵã���·�е��ܵ��ȣ� ![]()
��ֵ����R�����Ľ�����![]() ����ã�
����ã� ![]() ����D����ȷ��
����D����ȷ��
���ϴ�ΪCD��