题目内容
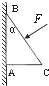
 横截面为直角三角形的两个相同斜面如图紧靠在一起,固定在水平面上,它们的竖直边长都是底边长的一半.小球从左边斜面的顶点以不同的初速度向右平抛,最后落在斜面上.其中有三次的落点分别是a、b、c.下列判断正确的是( )
横截面为直角三角形的两个相同斜面如图紧靠在一起,固定在水平面上,它们的竖直边长都是底边长的一半.小球从左边斜面的顶点以不同的初速度向右平抛,最后落在斜面上.其中有三次的落点分别是a、b、c.下列判断正确的是( )分析:平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,根据高度比较运动的时间,从而比较出速度变化量的大小.通过水平位移和时间比较平抛运动的初速度.
解答:解:A、根据h=
gt2知,a球下落的高度最大,则a球飞行的时间最长.故A错误.
B、根据h=
gt2知,a球下落的高度最大,则a球飞行的时间最长,根据△v=gt,知a球速度变化量最大.故B错误.
C、三个小球的加速度相等,则三个小球的速度变化快慢相同.故C错误.
D、c球下落的高度最小,则时间最短,c球的水平位移最大,则c球的初速度最大.故D正确.
故选D.
| 1 |
| 2 |
B、根据h=
| 1 |
| 2 |
C、三个小球的加速度相等,则三个小球的速度变化快慢相同.故C错误.
D、c球下落的高度最小,则时间最短,c球的水平位移最大,则c球的初速度最大.故D正确.
故选D.
点评:解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,知道平抛运动的时间由高度决定,初速度和时间共同决定水平位移.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 有一横截面为直角三角形的玻璃砖,a、b两束可见单色光从空气垂直斜面AC射向玻璃砖,两单色光在界面BC上的反射、折射情况如图所示.由此可知( )
有一横截面为直角三角形的玻璃砖,a、b两束可见单色光从空气垂直斜面AC射向玻璃砖,两单色光在界面BC上的反射、折射情况如图所示.由此可知( )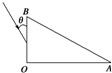 如图所示,一个横截面为直角三角形的三棱镜,∠A=30°,∠O=90°.三棱镜材料的折射率是n=
如图所示,一个横截面为直角三角形的三棱镜,∠A=30°,∠O=90°.三棱镜材料的折射率是n= 如图所示,一个横截面为直角三角形的三棱镜,∠A=30°,∠C=90°.三棱镜材料的折射率是.一束与BC面成θ=30°角的光线射向BC面.
如图所示,一个横截面为直角三角形的三棱镜,∠A=30°,∠C=90°.三棱镜材料的折射率是.一束与BC面成θ=30°角的光线射向BC面.