Question

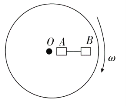
【题目】水平转台上有质量相等的A、B两小物块，两小物块间用沿半径方向的细线相连，两物块始终相对转台静止，其位置如图所示(俯视图)，两小物块与转台间的最大静摩擦力均为f0，则两小物块所受摩擦力FA、FB随转台角速度的平方(ω2)的变化关系正确的是( )

Answer 1

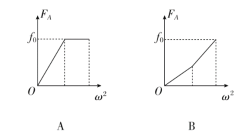
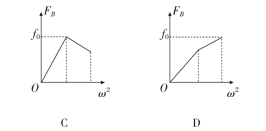
【答案】B

【解析】设A、B到圆心O的距离分别为r1、r2，若细线不存在，则由f0＝mω2r及r1<r2可知A、B两物体相对转台滑动的临界角速度满足ωA>ωB，即物体B所受摩擦力先达到最大值，随后在一段时间内保持不变，C、D错；当ω>ωB时，细线中出现拉力T，对物体A：T＝0时，FA＝mω2r1，T>0后，FA－T＝mω2r1，而对物体B满足T＋f0＝mω2r2，联立得FA＝mω2(r1＋r2)－f0，所以T>0后直线斜率比T＝0时大，当转台对A的摩擦力达到最大静摩擦力后，若转台角速度再增大，则A、B相对转台将出现滑动，所以A错、B对。