题目内容
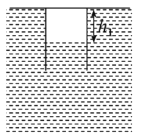
【题目】如图，将质量为 m、导热性良好的薄壁圆筒开口向下竖直缓慢地放入水中，筒内封闭了一定质量的气体(可视为理想气体)．当筒底与水面相平时，圆筒恰好静止在水中．此时水的温度t1=27 ℃ ，筒内气柱的长度 h1＝1m.已知大气压 p0＝1.0×105 Pa，水的密度 ρ＝1.0×10 3 kg/m3，重力加速度大小g取10m/s2
（ⅰ）若水温缓慢升高至42℃，求筒底露出水面的高度Δh为多少
（ⅱ）若水温保持 42℃不变，用手竖直向下缓慢压圆筒（封闭气体没有溢出），到某一深度后松手，气缸刚好静止（悬浮）在水中，求此时圆筒底部距离水面距离h
【答案】（i）
（ii）
【解析】
（i）初始时缸内气体温度
，长度
，水温升高至
过程，气体做等压变化，由盖-吕萨克定律有
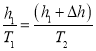①
得
（ii）初始时缸内气体压强为
，则有
②
得
移动圆筒后，由阿基米德定律有：气缸内气体长度仍为
，即体积不变，设此时气体压强为p，由查理定律有：
③
得
设圆筒内液面距离水面高度为
，则有
④
得
所以
⑤
得
练习册系列答案
相关题目
