题目内容
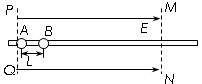
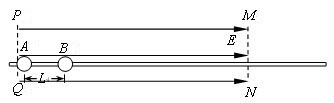
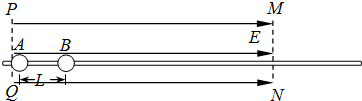 PQ、MN间存在匀强电场,场强为E,沿场强方向固定一绝缘细杆,杆上套有两个质量均为m的绝缘小球A、B,小球A带正电,电荷量为q,小球B不带电.将A、B从相距为L的两点由静止释放,之后A、B间的碰撞为弹性碰撞,碰撞时间极短且碰撞时没有电荷转移,运动中小球A的电荷量不变,求:
PQ、MN间存在匀强电场,场强为E,沿场强方向固定一绝缘细杆,杆上套有两个质量均为m的绝缘小球A、B,小球A带正电,电荷量为q,小球B不带电.将A、B从相距为L的两点由静止释放,之后A、B间的碰撞为弹性碰撞,碰撞时间极短且碰撞时没有电荷转移,运动中小球A的电荷量不变,求:(1)从A、B间的第一次碰撞到发生第二次碰撞,小球A运动的距离;
(2)若小球B出电场时的动能为16qEL,则A、B间发生了几次碰撞?
(3)若小球B出电场时的动能为16qEL,则小球A出电场时的动能多大?
分析:(1)A、B间发生弹性碰撞,遵守动量守恒和机械能守恒,根据两大守恒列式可知:由于质量相等,两球交换速度.先根据动能定理求出第一次碰撞前A的速度,根据碰撞的规律得到碰后两球的速度.再运用动能定理和运动学公式结合求解即可;
(2)运用动能定理和运动学公式结合,分别求出碰撞第二次、第三次碰撞后小球B出电场时的动能,即可判断A、B间发生了几次碰撞.
(3)若第四次碰撞发生后小球A即离开电场,对A球运用动能定理求解小球A出电场时的动能.若小球A在将要发生第五次碰撞时才离开电场,运用动能定理和运动学公式求解即可.
(2)运用动能定理和运动学公式结合,分别求出碰撞第二次、第三次碰撞后小球B出电场时的动能,即可判断A、B间发生了几次碰撞.
(3)若第四次碰撞发生后小球A即离开电场,对A球运用动能定理求解小球A出电场时的动能.若小球A在将要发生第五次碰撞时才离开电场,运用动能定理和运动学公式求解即可.
解答:解:A、B间发生弹性碰撞,设每次碰撞A、B的速度分别为v1、v2,碰后的速度分别为v′1、v′2,
由动量守恒定律和能量守恒定律得:
mv1+mv2=mv′1+mv′2 ①
m
+
m
=
mv
+
mv
②
联立①②解得 v′1=v2,v′2=v1或v′1=v1,v′2=v2(舍去),即每次碰撞两球都交换速度.
(1)设第一次碰撞前小球A的速度为v1,由动能定理得:qEL=
m
③
则第一次碰撞后 v′11=0,v′21=v11,小球A又开始做初速度为零的匀加速运动,小球B则以速度v1做匀速运动,设从A、B间的第一次碰撞到第二次碰撞前小球A运动的距离为L2,则
qEL2=
m
④
L2=v11t,L2=
t ⑤
联立③④⑤解得 v12=2v11,L2=4L
(2)第二次碰后v′12=v11,v′22=v12=2v11,设第三次碰撞前A运动的距离为L3,则 qEL3=
m
-
m
⑥
L3=v12t,L3=
t ⑦
联立解得:v13=3v11,L3=8L1=2L2
第三次碰后v′13=v12=2v11,v′23=v13=3v11,小球B的动能为Ek3=
m
=9
m
=32qEL,
因此当小球B出电场时的动能为16qEL=42qEL时,A、B间发生了四次碰撞.
(3)第四次碰撞后,小球A的速度v′14=v13=3v11,若第四次碰撞发生后小球A即离开电场,则A的动能 EkA=
m
=9qEL,
若小球A在将要发生第五次碰撞时才离开电场,则qEL5=E′kA-
m
⑧
L5=2(n-1)L2=8L2=16L ⑨
解得:E′kA=25qEL,故有 9qEL≤EkA<25qEL
答:
(1)从A、B间的第一次碰撞到发生第二次碰撞,小球A运动的距离为4L;
(2)若小球B出电场时的动能为16qEL,则A、B间发生了四次碰撞.
(3)若小球B出电场时的动能为16qEL,则小球A出电场时的动能为9qEL≤EkA<25qEL.
由动量守恒定律和能量守恒定律得:
mv1+mv2=mv′1+mv′2 ①
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
| ’ | 2 1 |
| 1 |
| 2 |
| ’ | 2 2 |
联立①②解得 v′1=v2,v′2=v1或v′1=v1,v′2=v2(舍去),即每次碰撞两球都交换速度.
(1)设第一次碰撞前小球A的速度为v1,由动能定理得:qEL=
| 1 |
| 2 |
| v | 2 11 |
则第一次碰撞后 v′11=0,v′21=v11,小球A又开始做初速度为零的匀加速运动,小球B则以速度v1做匀速运动,设从A、B间的第一次碰撞到第二次碰撞前小球A运动的距离为L2,则
qEL2=
| 1 |
| 2 |
| v | 2 12 |
L2=v11t,L2=
| v12 |
| 2 |
联立③④⑤解得 v12=2v11,L2=4L
(2)第二次碰后v′12=v11,v′22=v12=2v11,设第三次碰撞前A运动的距离为L3,则 qEL3=
| 1 |
| 2 |
| v | 2 13 |
| 1 |
| 2 |
| v | 2 11 |
L3=v12t,L3=
| v11+v13 |
| 2 |
联立解得:v13=3v11,L3=8L1=2L2
第三次碰后v′13=v12=2v11,v′23=v13=3v11,小球B的动能为Ek3=
| 1 |
| 2 |
| v | 2 13 |
| 1 |
| 2 |
| v | 2 11 |
因此当小球B出电场时的动能为16qEL=42qEL时,A、B间发生了四次碰撞.
(3)第四次碰撞后,小球A的速度v′14=v13=3v11,若第四次碰撞发生后小球A即离开电场,则A的动能 EkA=
| 1 |
| 2 |
| v | 2 13 |
若小球A在将要发生第五次碰撞时才离开电场,则qEL5=E′kA-
| 1 |
| 2 |
| v | 2 13 |
L5=2(n-1)L2=8L2=16L ⑨
解得:E′kA=25qEL,故有 9qEL≤EkA<25qEL
答:
(1)从A、B间的第一次碰撞到发生第二次碰撞,小球A运动的距离为4L;
(2)若小球B出电场时的动能为16qEL,则A、B间发生了四次碰撞.
(3)若小球B出电场时的动能为16qEL,则小球A出电场时的动能为9qEL≤EkA<25qEL.
点评:分析清楚物体的运动过程与运动性质,抓住两球弹性碰撞的基本规律:动量守恒和机械能守恒,两球质量相等会交换速度.再应用匀变速运动的速度公式、位移公式和动能定理即可正确解题.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
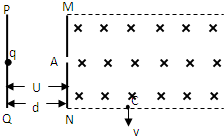 如图所示,PQ、MN两极板间存在匀强电场,两极板间电势差为U、间距为d,MN极板右侧虚线区域内有垂直纸面向内的匀强磁场.现有一初速度为零、带电量为q、质量为m的离子从PQ极板出发,经电场加速后,从MN上的小孔A垂直进入磁场区域,并从C点垂直于虚线边界射出.求:
如图所示,PQ、MN两极板间存在匀强电场,两极板间电势差为U、间距为d,MN极板右侧虚线区域内有垂直纸面向内的匀强磁场.现有一初速度为零、带电量为q、质量为m的离子从PQ极板出发,经电场加速后,从MN上的小孔A垂直进入磁场区域,并从C点垂直于虚线边界射出.求: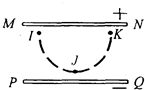 如图所示,水平放置的两个平行金属板MN、PQ间存在匀强电场和匀强磁场.MN板带正电,PQ板带负电,磁场方向垂直纸面向里.一带电微粒只在电场力和洛伦兹力作用下,从I点由静止开始沿曲线IJK运动,到达K点时速度为零,J是曲线上离MN板最远的点.有以下几种说法:
如图所示,水平放置的两个平行金属板MN、PQ间存在匀强电场和匀强磁场.MN板带正电,PQ板带负电,磁场方向垂直纸面向里.一带电微粒只在电场力和洛伦兹力作用下,从I点由静止开始沿曲线IJK运动,到达K点时速度为零,J是曲线上离MN板最远的点.有以下几种说法: