题目内容
（18分）如图所示，PQ、MN间存在匀强电场，场强为E，沿场强方向固定一个光滑绝缘细杆，杆上套有两个质量均为m的绝缘小球A、B，小球A带正电，电荷量为q，小球B不带电。将A、B从相距为L的两点由静止释放之后A、B间的碰撞没有动能损失，碰撞时间极短且碰撞时没有电荷转移，运动中小球A的电荷量不变，求：
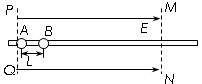
（1）从A、B间的第一次碰撞到发生第二次碰撞，小球A运动的距离（二者在此过程中没有离开电场）；
（2）若小球B刚离开电场时的动能为16qEL，则A、B间发生了几次碰撞？
解析：
（1）A、B间发生没有动能损失的碰撞，设每次碰撞前A、B的速度分别为v1、v2，碰后的速度分别为v1′、v2′，由动量守恒定律和能量守恒定律有
m v1+ m v2= m v1′+ m v2′ （2分）
（2分）
解得：v1′= v2 v2′= v1 即每次碰撞两球都交换速度
设第一次碰撞小球A的速度为v1，由动能定理得： 
（1分）
则第一次碰撞后v1′= 0 ，v2′= v1 小球A又开始做初速度为零的匀加速运动，小球B则以速度v1做匀速运动，设从A、B间的第一次碰撞到第二次碰撞前小球A运动的距离为L2，则，
（1分）
L2= v1t （1分）
L2= v12t /2 （1分）
解得： v12=2 v1 （1分）
L2= 4L （1分）
（2）由（1）中可知，第一次碰后小球B的动能
（1分）
第二次碰撞后 v12′= v1 v22′= v12=2 v1
第三次碰撞前小球A运动的距离为L3，则
（1分）
L3= v12t 
联立得v13′=3 v1 L3= 8L= 2L2 （1分）
第二次碰后小球B的动能
（2分）
同理：第三次碰后小球B的动能
当小球B出电场时的动能为 16qEL= 42 qEL
所以A、B间发生了4次碰撞。（3分）
名校课堂系列答案
如图所示，PQ和MN为水平放置的平行金属导轨，间距为L=1.0m，导体棒ab跨放在导轨上，棒的质量为m=20g，棒的中点用细绳经轻滑轮与物体c相连，物体c的质量M=30g，悬在空中．在垂直导轨平面方向存在磁感应强度B=0.2T的匀强磁场，磁场方向竖直向上，重力加速度g取10m/s2．若导轨是粗糙的，且导体棒与导轨间的最大静摩擦力为导体棒ab重力的0.5倍，若要保持物体c静止不动，应该在棒中通入电流方向如何？电流大小的范围是多少？
如图所示，PQ和MN为水平放置的光滑的平行金属导轨，间距为l=1.0m，导体棒ab垂直跨放在导轨上，棒的质量为m=2kg，棒的中点用细绳经轻滑轮与质量为M=0.2kg的物体相连，物体M放在倾角为θ=30°的固定的斜面上，与M连接的轻绳与斜面平行．整个装置区域存在一个方向与导体棒垂直且与水平面的夹角α=53°斜向左上方的匀强磁场，重力加速度g10m/s2取．若磁感应强度B=0.5T，物块M与斜面之间的动摩擦因素μ=
如图所示，PQ和MN为水平平行放置的金属导轨，相距L=1m．PM间接有一个电动势为E=6V，内阻r=1Ω的电源和一只滑动变阻器．导体棒ab跨放在导轨上，棒的质量为m=0.2kg，棒的中点用细绳经定滑轮与物体相连，物体的质量M=0.3kg．棒与导轨的动摩擦因数为μ=0.5（设最大静摩擦力与滑动摩擦力相等，导轨与棒的电阻不计，g取10m/s2），匀强磁场的磁感应强度B=2T，方向竖直向下，为了使物体保持静止，滑动变阻器连入电路的阻值不可能的是（ ）
如图所示，PQ和MN为水平平行放置的金属导轨，相距L=1m．PM间接有一个电动势为E=6V，内阻r=1Ω的电源和一只滑动变阻器．导体棒ab跨放在导轨上，棒的质量为m=0.2kg，棒的中点用细绳经定滑轮与物体相连，物体的质量M=0.3kg．棒与导轨的动摩擦因数为μ=0.5（设最大静摩擦力与滑动摩擦力相等，导轨与棒的电阻不计，g取10m/s2），匀强磁场的磁感应强度B=2T，方向竖直向下，为了使物体保持静止，滑动变阻器连入电路的阻值不可能是（ ）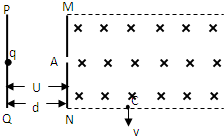
如图所示，PQ、MN两极板间存在匀强电场，两极板间电势差为U、间距为d，MN极板右侧虚线区域内有垂直纸面向内的匀强磁场．现有一初速度为零、带电量为q、质量为m的离子从PQ极板出发，经电场加速后，从MN上的小孔A垂直进入磁场区域，并从C点垂直于虚线边界射出．求：