Question

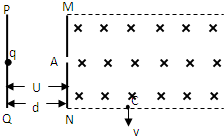如图所示，PQ、MN两极板间存在匀强电场，两极板间电势差为U、间距为d，MN极板右侧虚线区域内有垂直纸面向内的匀强磁场．现有一初速度为零、带电量为q、质量为m的离子从PQ极板出发，经电场加速后，从MN上的小孔A垂直进入磁场区域，并从C点垂直于虚线边界射出．求：
（1）离子从小孔A射出时速度v0；
（2）离子带正电还是负电？C点离MN板的距离？

Answer 1

分析：（1）离子在电场中加速时，电场力做功为qU，根据动能定理求解离子从小孔A射出时速度v₀；
（2）离子进入磁场后向下偏转，则知所受的洛伦兹力方向向下，由左手定则判断离子的电性．离子在磁场中由洛伦兹力提供向心力，由牛顿第二定律求出轨迹的半径，由几何关系求出C点离MN板的距离．

解答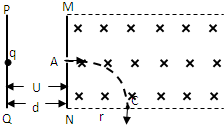：解：（1）由动能定理得：qU=

1

2

m

v

2 0

解得，离子从小孔A射出时速度为  v₀=

2qU m

（2）由左手定则可知离子带负电．离子进入磁场后，洛仑兹力提供向心力，由牛顿第二定律得：
   qv₀B=m

v 2 0

r

解得：r=

mv0

qB

=

1

B

2mU q

所以C点离MN板的距离为

1

B

2mU q

．
答：
（1）离子从小孔A射出时速度v₀是

2qU m

．
（2）离子带负电，C点离MN板的距离为

1

B

2mU q

．

点评：本题中带电粒子先加速后由磁场偏转，根据动能定理求加速获得的速度，画出磁场中粒子的运动轨迹是处理这类问题的基本方法．