题目内容
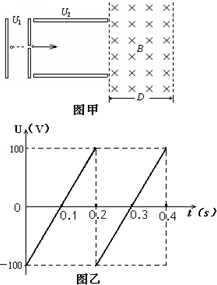 如图甲所示,一个质量为m=2.0×10-11kg,电荷量q=+1.0×10-5C的带电微粒(重力忽略不计),从静止开始经U1=100V电压加速后,水平进入两平行金属板间的偏转电场,偏转电场的电压如图乙所示.金属板长L=20cm,两板间距d=10
如图甲所示,一个质量为m=2.0×10-11kg,电荷量q=+1.0×10-5C的带电微粒(重力忽略不计),从静止开始经U1=100V电压加速后,水平进入两平行金属板间的偏转电场,偏转电场的电压如图乙所示.金属板长L=20cm,两板间距d=10| 3 |
(1)微粒射出偏转电场时的最大偏转角θ;
(2)若紧靠偏转电场边缘有一边界垂直金属板的匀强磁场,该磁场的宽度为D=10cm,为使微粒无法由磁场右边界射出,该匀强磁场的磁感应强度B应满足什么条件?
(3)试求在上述B取最小值的情况下,微粒离开磁场的范围.
分析:(1)微粒先经加速电场加速,后进入偏转电场偏转做类平抛运动,最后进入磁场中做匀速圆周运动.先根据动能定理列式,得出加速获得的速度.运用运动的分解,根据牛顿第二定律和运动学公式结合得出射出电场时的偏转角正切表达式,再分析求解最大偏转角θ;
(2)当微粒在磁场中的运动轨迹恰好与磁场右边界相切时,恰好不能射出磁场,画出轨迹,由几何知识求出轨迹半径,由牛顿第二定律求出B的最小值.
(3)根据几何知识求解微粒离开磁场的范围.
(2)当微粒在磁场中的运动轨迹恰好与磁场右边界相切时,恰好不能射出磁场,画出轨迹,由几何知识求出轨迹半径,由牛顿第二定律求出B的最小值.
(3)根据几何知识求解微粒离开磁场的范围.
解答: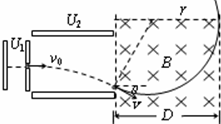
 解:(1)微粒在加速电场中由动能定理得:
解:(1)微粒在加速电场中由动能定理得:
qU1=
m
①
解得v0=1.0×104m/s
微粒在偏转电场中运动的时间为:t=
=2×10-5s<<0.2s
因此微粒在偏转电场中运动可认为电场恒定.
微粒在偏转电场中做类平抛运动,有:a=
,vy=at=a
飞出电场时,速度偏转角的正切为:
tanθ=
联立解得tanθ=
②
当U2最大时,tanθ最大,由图乙读出U2最大值为100V,代入解得tanθ最大值为
,解得θ的最大值为30°.
(2)进入磁场时微粒的速度是:v=
③
轨迹如图,由几何关系有:D=r+rsinθ ④
由洛伦兹力提供向心力:qvB=m
⑤
由③~⑤联立得:B=
代入数据解得:B=
T=0.346T
所以,为使微粒不会由磁场右边射出,该匀强磁场的磁感应强度B至少为0.346T.
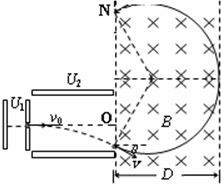
(3)设微粒从左边界N处离开,N距轴线与磁场边界交点O的距离为x,有:
可见,在B取最小值时,x仅与U2有关.代入数值可得:
X∈[
m,
m].
答:
(1)微粒射出偏转电场时的最大偏转角θ是30°.
(2)该匀强磁场的磁感应强度B至少为0.346T.
(3)在上述B取最小值的情况下,微粒离开磁场的范围是X∈【
m,
m】.

 解:(1)微粒在加速电场中由动能定理得:
解:(1)微粒在加速电场中由动能定理得:qU1=
| 1 |
| 2 |
| v | 2 0 |
解得v0=1.0×104m/s
微粒在偏转电场中运动的时间为:t=
| L |
| v0 |
因此微粒在偏转电场中运动可认为电场恒定.
微粒在偏转电场中做类平抛运动,有:a=
| qU2 |
| md |
| L |
| v0 |
飞出电场时,速度偏转角的正切为:
tanθ=
| vy |
| v0 |
联立解得tanθ=
| U2L |
| 2U1d |
当U2最大时,tanθ最大,由图乙读出U2最大值为100V,代入解得tanθ最大值为
| ||
| 3 |
(2)进入磁场时微粒的速度是:v=
| v0 |
| cosθ |
轨迹如图,由几何关系有:D=r+rsinθ ④
由洛伦兹力提供向心力:qvB=m
| v2 |
| r |
由③~⑤联立得:B=
| mv0(1+sinθ) |
| qDcosθ |
代入数据解得:B=
| ||
| 5 |
所以,为使微粒不会由磁场右边射出,该匀强磁场的磁感应强度B至少为0.346T.
(3)设微粒从左边界N处离开,N距轴线与磁场边界交点O的距离为x,有:
|
可见,在B取最小值时,x仅与U2有关.代入数值可得:
X∈[
| ||
| 30 |
| ||
| 10 |
答:
(1)微粒射出偏转电场时的最大偏转角θ是30°.
(2)该匀强磁场的磁感应强度B至少为0.346T.
(3)在上述B取最小值的情况下,微粒离开磁场的范围是X∈【
| ||
| 30 |
| ||
| 10 |
点评:本题是带电粒子的复合场中运动的类型,关键要分析出微粒的运动情况,作出粒子的运动轨迹,根据几何知识得到轨迹半径与磁场边界半径的关系.

练习册系列答案
相关题目
光滑水平面上放置两个等量同种电荷,其连线中垂线上有A、B、C三点,如图甲所示,一个质量m=1kg的小物块自C点由静止释放,小物块带电荷量q=2C,其运动的v-t图线如图乙所示,其中B点为整条图线切线斜率最大的位置(图中标出了该切线),则以下分析正确的是( )


| A、B点为中垂线上电场强度最大的点,场强E=1V/m | B、由C点到A点物块的电势能先减小后变大 | C、由C点到A点,电势逐渐降低 | D、B、A两点间的电势差为UBA=8.25V |
 如图甲所示,一个质量为m,带电量为q的离子,从D点以某一初速度垂直进入匀强磁场.磁场方向垂直纸面向内,磁感应强度为B.正离子的初速度方向在纸面内,与直线AD的夹角为60°.结果粒子正好穿过AD的垂线上离A点距离为d的小孔C,垂直AC的方向进入AC右边的匀强电场中.电场的方向与AC平行.离子最后打在DA直线上的P点.P到A的距离为2d.不计重力,
如图甲所示,一个质量为m,带电量为q的离子,从D点以某一初速度垂直进入匀强磁场.磁场方向垂直纸面向内,磁感应强度为B.正离子的初速度方向在纸面内,与直线AD的夹角为60°.结果粒子正好穿过AD的垂线上离A点距离为d的小孔C,垂直AC的方向进入AC右边的匀强电场中.电场的方向与AC平行.离子最后打在DA直线上的P点.P到A的距离为2d.不计重力, 如图甲所示,一个质量为M=1kg的物块静止在粗糙水平面上的A点,从t=0时刻开始,物块在按如图乙所示规律变化的水平力F的作用下向右运动,第3s末,物块运动到B点,且速度刚好为0,第5s末,物块刚好回到A点.物块与粗糙水平面间的动摩擦因数μ=0.3,g取10m/s2,则以下说法正确的是( )
如图甲所示,一个质量为M=1kg的物块静止在粗糙水平面上的A点,从t=0时刻开始,物块在按如图乙所示规律变化的水平力F的作用下向右运动,第3s末,物块运动到B点,且速度刚好为0,第5s末,物块刚好回到A点.物块与粗糙水平面间的动摩擦因数μ=0.3,g取10m/s2,则以下说法正确的是( )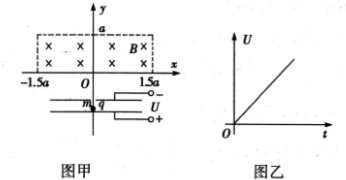 如图甲所示,一个质量为m,电荷量为+q的微粒(不计重力),初速度为零,经两金属板间电场加速后,沿y轴射入一个边界为矩形的匀强磁场中,磁场方向垂直纸面向里.磁场的四条边界分别是y=0,y=a,x=-1.5a,x=1.5a.两金属板间电压随时间均匀增加,如图乙所示.由于两金属板间距很小,微粒在电场中运动时间极短,可认为微粒在加速运动过程中电场恒定.
如图甲所示,一个质量为m,电荷量为+q的微粒(不计重力),初速度为零,经两金属板间电场加速后,沿y轴射入一个边界为矩形的匀强磁场中,磁场方向垂直纸面向里.磁场的四条边界分别是y=0,y=a,x=-1.5a,x=1.5a.两金属板间电压随时间均匀增加,如图乙所示.由于两金属板间距很小,微粒在电场中运动时间极短,可认为微粒在加速运动过程中电场恒定.