题目内容
 如图甲所示,一个质量为M=1kg的物块静止在粗糙水平面上的A点,从t=0时刻开始,物块在按如图乙所示规律变化的水平力F的作用下向右运动,第3s末,物块运动到B点,且速度刚好为0,第5s末,物块刚好回到A点.物块与粗糙水平面间的动摩擦因数μ=0.3,g取10m/s2,则以下说法正确的是( )
如图甲所示,一个质量为M=1kg的物块静止在粗糙水平面上的A点,从t=0时刻开始,物块在按如图乙所示规律变化的水平力F的作用下向右运动,第3s末,物块运动到B点,且速度刚好为0,第5s末,物块刚好回到A点.物块与粗糙水平面间的动摩擦因数μ=0.3,g取10m/s2,则以下说法正确的是( )分析:在前3s,由于物体受到的拉力是变化的,物体做变速运动,但是在3s-5s的时间内,物体受到恒力的作用做匀加速直线运动,根据物体的运动过程,可以求得拉力做功的大小及物体最后的速度的大小.
解答:解:在3s-5s的时间内,物块在水平恒力F的作用下由B点匀加速直线运动到A点,
设加速度为a,AB间的距离为s,则:F-μMg=Ma,
所以a=
=
m/s2=1m/s2
则位移的大小x=
at2=
×1×4m=2m.
第5s末的速度v=at=2m/s,则动能为Ek=
Mv2=
×1×4J=2J.
整个过程中克服摩擦力做的功为Wf=2μMgs=2×0.3×10×2J=12J.故A错误,B正确.
C、根据动能定理得,WF-Wf=
mv2-0,解得WF=Wf+
Mv2=12+2J=14J,则平均功率P=
=
W=2.8W.故C错误.
D、对A到B运用动能定理得,WF-μmgs=0,则WF=μMgs=0.3×10×2J=6J.故D错误.
故选B.
设加速度为a,AB间的距离为s,则:F-μMg=Ma,
所以a=
| F-μMg |
| M |
| 4-0.3×10 |
| 1 |
则位移的大小x=
| 1 |
| 2 |
| 1 |
| 2 |
第5s末的速度v=at=2m/s,则动能为Ek=
| 1 |
| 2 |
| 1 |
| 2 |
整个过程中克服摩擦力做的功为Wf=2μMgs=2×0.3×10×2J=12J.故A错误,B正确.
C、根据动能定理得,WF-Wf=
| 1 |
| 2 |
| 1 |
| 2 |
| WF |
| t |
| 14 |
| 5 |
D、对A到B运用动能定理得,WF-μmgs=0,则WF=μMgs=0.3×10×2J=6J.故D错误.
故选B.
点评:在前3s内物体是做变速运动,不能分析物体的运动规律,但是根据动能定理可以知道,此时拉力的功与摩擦力做的功大小相同,本题的关键是对物体的第二个运动过程的分析.

练习册系列答案
相关题目
光滑水平面上放置两个等量同种电荷,其连线中垂线上有A、B、C三点,如图甲所示,一个质量m=1kg的小物块自C点由静止释放,小物块带电荷量q=2C,其运动的v-t图线如图乙所示,其中B点为整条图线切线斜率最大的位置(图中标出了该切线),则以下分析正确的是( )


| A、B点为中垂线上电场强度最大的点,场强E=1V/m | B、由C点到A点物块的电势能先减小后变大 | C、由C点到A点,电势逐渐降低 | D、B、A两点间的电势差为UBA=8.25V |
 如图甲所示,一个质量为m,带电量为q的离子,从D点以某一初速度垂直进入匀强磁场.磁场方向垂直纸面向内,磁感应强度为B.正离子的初速度方向在纸面内,与直线AD的夹角为60°.结果粒子正好穿过AD的垂线上离A点距离为d的小孔C,垂直AC的方向进入AC右边的匀强电场中.电场的方向与AC平行.离子最后打在DA直线上的P点.P到A的距离为2d.不计重力,
如图甲所示,一个质量为m,带电量为q的离子,从D点以某一初速度垂直进入匀强磁场.磁场方向垂直纸面向内,磁感应强度为B.正离子的初速度方向在纸面内,与直线AD的夹角为60°.结果粒子正好穿过AD的垂线上离A点距离为d的小孔C,垂直AC的方向进入AC右边的匀强电场中.电场的方向与AC平行.离子最后打在DA直线上的P点.P到A的距离为2d.不计重力,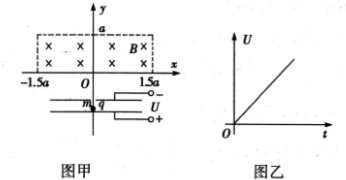 如图甲所示,一个质量为m,电荷量为+q的微粒(不计重力),初速度为零,经两金属板间电场加速后,沿y轴射入一个边界为矩形的匀强磁场中,磁场方向垂直纸面向里.磁场的四条边界分别是y=0,y=a,x=-1.5a,x=1.5a.两金属板间电压随时间均匀增加,如图乙所示.由于两金属板间距很小,微粒在电场中运动时间极短,可认为微粒在加速运动过程中电场恒定.
如图甲所示,一个质量为m,电荷量为+q的微粒(不计重力),初速度为零,经两金属板间电场加速后,沿y轴射入一个边界为矩形的匀强磁场中,磁场方向垂直纸面向里.磁场的四条边界分别是y=0,y=a,x=-1.5a,x=1.5a.两金属板间电压随时间均匀增加,如图乙所示.由于两金属板间距很小,微粒在电场中运动时间极短,可认为微粒在加速运动过程中电场恒定.