题目内容
（2008?烟台一模）如图甲所示，一个质量为m、电荷量q的带正电微料（重力忽略不计），从静止开始经电压U1加速后，沿水平方向进入两等大的水平放置的平行金属板间，金属板长为L，两板间距d=L/4，两金属板间的电压U2=
U1，求：
（1）求带电微粒偏离原来运动方向的角度θ为多大？
（2）微粒离开偏转电场后接着进入一个按图乙规律变化的有界磁场中，磁场左右边线在竖直方向上，已知磁感应强度的大小为B0，取微粒刚进入磁场时为t=0时刻，此时磁场方向垂直于纸面向里，当微粒离开磁场的右边缘后恰好沿竖直方向运动，求该磁场的变化周期T为多大？（微粒在磁场中运动的时间t＜T）
| ||
| 6 |
（1）求带电微粒偏离原来运动方向的角度θ为多大？
（2）微粒离开偏转电场后接着进入一个按图乙规律变化的有界磁场中，磁场左右边线在竖直方向上，已知磁感应强度的大小为B0，取微粒刚进入磁场时为t=0时刻，此时磁场方向垂直于纸面向里，当微粒离开磁场的右边缘后恰好沿竖直方向运动，求该磁场的变化周期T为多大？（微粒在磁场中运动的时间t＜T）
分析：（1）粒子在加速电场中，电场力做功，由动能定理求出初速度，粒子进入偏转电场后，做类平抛运动，运用运动的合成与分解求出偏转角；
（2）粒子进入磁场后，做匀速圆周运动，结合条件，画出轨迹，由几何知识结合周期公式即可求解．
（2）粒子进入磁场后，做匀速圆周运动，结合条件，画出轨迹，由几何知识结合周期公式即可求解．
解答：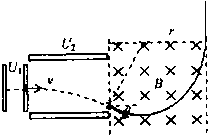
解：（1）加速过程qU1=
m
偏转过程a=
竖直分速度为v2=at
水平方向l=v1t
设偏转角度为θ，则tanθ=
解得θ=30°
（2）轨迹如图所示，带电粒子在磁场中做匀
速圆周运动的周期为T1=
由几何关系可知轨迹对应的圆心角为α=120°
此过程粒子运动的时间为
T1
∴磁场磁感应强度变化的周期为T=
答：（1）求带电微粒偏离原来运动方向的角度θ为30°；
（2）该磁场的变化周期T为
．
解：（1）加速过程qU1=| 1 |
| 2 |
| v | 2 1 |
偏转过程a=
| qU2 |
| md |
竖直分速度为v2=at
水平方向l=v1t
设偏转角度为θ，则tanθ=
| v2 |
| v1 |
解得θ=30°
（2）轨迹如图所示，带电粒子在磁场中做匀
速圆周运动的周期为T1=
| 2πm |
| qB0 |
由几何关系可知轨迹对应的圆心角为α=120°
此过程粒子运动的时间为
| 1 |
| 3 |
∴磁场磁感应强度变化的周期为T=
| 4πm |
| 3qB0 |
答：（1）求带电微粒偏离原来运动方向的角度θ为30°；
（2）该磁场的变化周期T为
| 4πm |
| 3qB0 |
点评：本题是带电粒子在组合场中运动的问题，关键是分析粒子的受力情况和运动情况，用力学的方法处理．
练习册系列答案
相关题目
（2008?烟台一模）如图所示，弹簧秤外壳质量为m，弹簧及挂钩的质量忽略不计，挂钩上吊一重物．现用一竖直向上的外力拉弹簧秤，当弹簧秤向上做匀速直线运动时，示数为F1；若让弹簧秤以加速度a向上做匀加速直线运动，则弹簧秤的示数为（重力加速度为g）（ ）
（2008?烟台一模）如图在竖直方向上的两个匀强磁场B1和B2中，各放入一个完全一样的水平金属圆盘a和b，它们可绕竖直轴自由转动，用导线将a盘中心与b盘边缘相连，b盘中心与a盘边缘相连，当a盘转动时，导线不动，则（ ）