题目内容
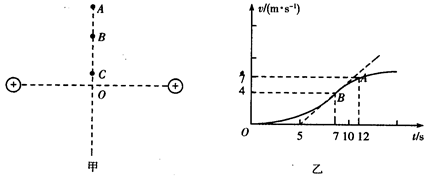
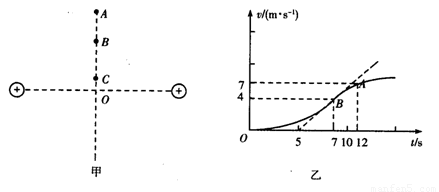
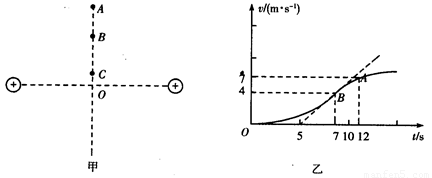
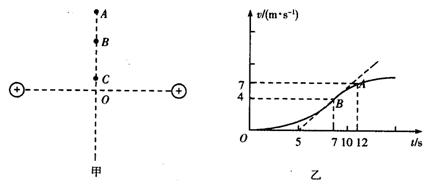
光滑水平面上放置两个等量同种电荷,其连线中垂线上有A、B、C三点,如图甲所示,一个质量m=1kg的小物块自C点由静止释放,小物块带电荷量q=2C,其运动的v-t图线如图乙所示,其中B点为整条图线切线斜率最大的位置(图中标出了该切线),则以下分析正确的是( )


| A、B点为中垂线上电场强度最大的点,场强E=1V/m | B、由C点到A点物块的电势能先减小后变大 | C、由C点到A点,电势逐渐降低 | D、B、A两点间的电势差为UBA=8.25V |
分析:根据v-t图象的斜率等于加速度和牛顿第二定律求解电场强度E.根据能量守恒定律分析物块电势能的变化情况.根据电场线方向判断电势的高低.根据动能定理求解AB两点电势差UAB.
解答:解:A、v-t图象的斜率等于加速度,B点处为整条图线切线斜率最大的位置,说明物块在B处加速度最大,根据牛顿第二定律得:
F=qE=ma,B为中垂线上电场强度最大的点,由图得:B点的加速度为 a=
=
=2m/s2,E=
=
V/m=lV/m.故A正确.
B、由图知,由C到A的过程中,物块的速度不断增大,动能增大,根据能量守恒得:物块的电势能不断减小.故B错误.
C、由电势能的公式EP=qφ知,由C到A的过程中,电势逐渐降低,故C正确.
D、物块从A到B的过程,根据动能定理得:qUAB=
mvB2-
mvA2,则得,UAB=
m(
-
)=
×(42-72)=-8.25V,所以UBA=-UAB=8.25V,故D正确.
故选:ACD
F=qE=ma,B为中垂线上电场强度最大的点,由图得:B点的加速度为 a=
| △v |
| △t |
| 4 |
| 2 |
| ma |
| q |
| 1×2 |
| 2 |
B、由图知,由C到A的过程中,物块的速度不断增大,动能增大,根据能量守恒得:物块的电势能不断减小.故B错误.
C、由电势能的公式EP=qφ知,由C到A的过程中,电势逐渐降低,故C正确.
D、物块从A到B的过程,根据动能定理得:qUAB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2q |
| v | 2 B |
| v | 2 A |
| 1 |
| 2×2 |
故选:ACD
点评:解决本题的关键是掌握速度图象的物理意义和动能定理,知道电势与电势能的关系EP=qφ.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目