题目内容
 (2009?德阳模拟)在光滑水平面上有两个可视为质点的小球A、B,mA=1kg,mB=0.5kg在两球间存在一有限区域:当两小球均在该区域内或者任一小球在该区域内两球间就有相互作用的恒定斥力F=1N,当两小球均在该区域外时两球间无作用力.A球离作用区左边界SA=20m,B在作用区右边界处,作用区长度L=5.5m.现使A以初速度vA=8m/s、B球以初速度vB=2m/s相向运动.求:
(2009?德阳模拟)在光滑水平面上有两个可视为质点的小球A、B,mA=1kg,mB=0.5kg在两球间存在一有限区域:当两小球均在该区域内或者任一小球在该区域内两球间就有相互作用的恒定斥力F=1N,当两小球均在该区域外时两球间无作用力.A球离作用区左边界SA=20m,B在作用区右边界处,作用区长度L=5.5m.现使A以初速度vA=8m/s、B球以初速度vB=2m/s相向运动.求:(1)A从开始运动到完全穿过作用区所用时间
(2)适当调节作用区的宽度或作用力大小,可使A穿过作用区后A、B两球的总动能最小,求A、B两球的最小总动能.
分析:(1)A从开始运动到完全穿过作用区时,两球间存在相互作用力,大小为F,A球做匀减速运动,B球做匀减速运动,根据牛顿第二定律可求得两球的加速度大小.根据运动学公式求出B在作用区中运动的最远距离.对B,运用动量定理求出B从进入作用区到穿出作用区的时间,运用运动学公式求出A运动匀减速运动的距离,再求解匀速运动的时间,分过程求解.
(2)要使A、B的动能之和最小,A穿过作用区后与B速度相等,即可求得A、B两球的最小总动能.
(2)要使A、B的动能之和最小,A穿过作用区后与B速度相等,即可求得A、B两球的最小总动能.
解答:解:(1)B球受作用力的加速度为:aB=
=
m/s2=2m/s2
A球受作用力的加速度为:aA=
=
m/s2=1m/s2
B在作用区中运动的最远距离为:Sm=
=
m=1m
B从进入作用区到穿出作用区用时有:Ft1=2mBvB
代人数据解得:t1=
=
s=2s
A运动匀减速运动的距离为:S1=vAt1-
aA
=(8×2-
×1×22)m=14m
A的速度为:v1=vA-aAt1=(8-1×2)m/s=6m/s
A匀速运动的时间为:t2=
=
s=1s
A穿出作用区用时为:L=v1t3-
aA
代人数据得:5.5=6×t3-
×1×
解得,t3=1s (另一解t3=11s,因A做匀减速运动,速度减小,若t3=11s,A穿过相互作用区时,速度为:v3=v1-aAt3=6-1×11=-5m/s,说明A回头,不能穿过相互作用区,不合理,故舍去)
故A从开始运动到完全穿过作用区所用时间为:t=t1+t2+t3=4s
(2)要使A、B的动能之和最小,则A穿过作用区后与B速度相等
右动量守恒得:mAvA-mBvB=(mA+mB)v
A、B的动能之和为:Ek=
(mA+mB)v2
解得:Ek=16.3J
答:(1)A从开始运动到完全穿过作用区所用时间为4s.
(2)A、B两球的最小总动能为16.3J.
| F |
| mB |
| 1 |
| 0.5 |
A球受作用力的加速度为:aA=
| F |
| mA |
| 1 |
| 1 |
B在作用区中运动的最远距离为:Sm=
| ||
| 2aB |
| 22 |
| 2×2 |
B从进入作用区到穿出作用区用时有:Ft1=2mBvB
代人数据解得:t1=
| 2mBvB |
| F |
| 2×0.5×2 |
| 1 |
A运动匀减速运动的距离为:S1=vAt1-
| 1 |
| 2 |
| t | 2 1 |
| 1 |
| 2 |
A的速度为:v1=vA-aAt1=(8-1×2)m/s=6m/s
A匀速运动的时间为:t2=
| SA-S1 |
| v1 |
| 20-14 |
| 6 |
A穿出作用区用时为:L=v1t3-
| 1 |
| 2 |
| t | 2 3 |
代人数据得:5.5=6×t3-
| 1 |
| 2 |
| t | 2 3 |
解得,t3=1s (另一解t3=11s,因A做匀减速运动,速度减小,若t3=11s,A穿过相互作用区时,速度为:v3=v1-aAt3=6-1×11=-5m/s,说明A回头,不能穿过相互作用区,不合理,故舍去)
故A从开始运动到完全穿过作用区所用时间为:t=t1+t2+t3=4s
(2)要使A、B的动能之和最小,则A穿过作用区后与B速度相等
右动量守恒得:mAvA-mBvB=(mA+mB)v
A、B的动能之和为:Ek=
| 1 |
| 2 |
解得:Ek=16.3J
答:(1)A从开始运动到完全穿过作用区所用时间为4s.
(2)A、B两球的最小总动能为16.3J.
点评:本题分析清楚A、B运动的过程是关键,运用牛顿第二定律和运动学公式结合进行判断.

练习册系列答案
相关题目
 (2009?德阳模拟)如图虚线a、b、c代表电场中的三条等势线,相邻两等势线之间的电势差相等,实线为一带正电的微粒仅在电场力作用下通过该区域时的运动轨迹,P、Q是这条轨迹上的两点,P、Q相比( )
(2009?德阳模拟)如图虚线a、b、c代表电场中的三条等势线,相邻两等势线之间的电势差相等,实线为一带正电的微粒仅在电场力作用下通过该区域时的运动轨迹,P、Q是这条轨迹上的两点,P、Q相比( ) (2009?德阳模拟)一平行板电容器充电后与电源断开,正极板接地,在两极板间有一正电荷(电量很小)固定在P点,如图所示.以E表示两极板间的场强,U表示电容器的电压,ε表示正电荷在P点的电势能,若保持负极板不动,将正极板移到图中虚线所示的位置,则( )
(2009?德阳模拟)一平行板电容器充电后与电源断开,正极板接地,在两极板间有一正电荷(电量很小)固定在P点,如图所示.以E表示两极板间的场强,U表示电容器的电压,ε表示正电荷在P点的电势能,若保持负极板不动,将正极板移到图中虚线所示的位置,则( ) (2009?德阳模拟)如图,把一个带电小球A固定在光滑的水平绝缘桌面上,在桌面的另一处放置带电小球B.现给B一个沿垂直AB方向的速度v0,下列说法中正确的是( )
(2009?德阳模拟)如图,把一个带电小球A固定在光滑的水平绝缘桌面上,在桌面的另一处放置带电小球B.现给B一个沿垂直AB方向的速度v0,下列说法中正确的是( )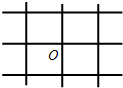 (2009?德阳模拟)如图为蹦床运动员的蹦床示意图,网绳的结构为正方格形,某次质量为m的运动员从高处落下,并恰好落在中心O,该处下凹至最低点时周围四根网绳均与竖直方向成600角,此时O点受到向下的冲击力为F,则O点周围每根网绳所受冲击力大小为( )
(2009?德阳模拟)如图为蹦床运动员的蹦床示意图,网绳的结构为正方格形,某次质量为m的运动员从高处落下,并恰好落在中心O,该处下凹至最低点时周围四根网绳均与竖直方向成600角,此时O点受到向下的冲击力为F,则O点周围每根网绳所受冲击力大小为( )