题目内容
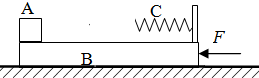 (2008?荆州一模)如图所示.质量为M=6kg的滑饭静止在光滑水平面上,滑板的右端固定一轻弹簧.在滑板的最左端放一可视为质点的小物体A,弹簧的自由端C与A相距L=1m.弹簧下面的那段滑板是光滑的,C左侧的那段滑板是粗糙的,物体A与这段粗糙滑板间的动摩擦因数为μ=0.2,A的质量m=2kg.滑板受到水平向左恒力F作用1s后撤去,撤去水平力F时A好滑到C处,g取10m/s2,求:
(2008?荆州一模)如图所示.质量为M=6kg的滑饭静止在光滑水平面上,滑板的右端固定一轻弹簧.在滑板的最左端放一可视为质点的小物体A,弹簧的自由端C与A相距L=1m.弹簧下面的那段滑板是光滑的,C左侧的那段滑板是粗糙的,物体A与这段粗糙滑板间的动摩擦因数为μ=0.2,A的质量m=2kg.滑板受到水平向左恒力F作用1s后撤去,撤去水平力F时A好滑到C处,g取10m/s2,求:(1)恒力F作用的这1s内小物体A的加速度为多大?位移为多大?
(2)作用力F的大小;
(3)A压缩弹簧过程中弹簧的最大弹性势能Ep;
(4)试分析判断在A撤去后,小物体能否与滑板相分离?若能,分离后物体和滑板的速度各为多大?若不能,小物体将停止在滑板上的什么位置?
分析:(1)根据牛顿第二定律求解A的加速度.由位移公式求解位移.
(2)对滑板B研究,先求出1s内滑板B的位移为SB=SA+L,再根据位移公式求解其加速度,由牛顿第二定律求解F的大小.
(3)撤去水平力F后,当A、B速度相等时弹簧的弹性势能最大,根据动量守恒和能量守恒结合求解.
(4)撤去F后,当弹簧恢复原长过程中,运用动量守恒和能量守恒列式求出此时A、B的速度,之后A做减速运动,B做加速运动,假设它们能达到共同速度,根据动量守恒和能量守恒列式求出共同速度和两者相对位移,根据相对位移与板长的关系判断即可.
(2)对滑板B研究,先求出1s内滑板B的位移为SB=SA+L,再根据位移公式求解其加速度,由牛顿第二定律求解F的大小.
(3)撤去水平力F后,当A、B速度相等时弹簧的弹性势能最大,根据动量守恒和能量守恒结合求解.
(4)撤去F后,当弹簧恢复原长过程中,运用动量守恒和能量守恒列式求出此时A、B的速度,之后A做减速运动,B做加速运动,假设它们能达到共同速度,根据动量守恒和能量守恒列式求出共同速度和两者相对位移,根据相对位移与板长的关系判断即可.
解答:解:(1)用字母B表示滑板,在这1s内滑板B和小物体A均向左做匀加速运动,对A有:
aA=
=μg=0.2×10=2m/s2
则位移为:SA=
aAt2=
×2×12=1m
(2)这1S内滑板B的位移为:SB=SA+L=1+1=2m
对B有:SB=
aBt2
得:aB=
=
=4m/s2
根据牛顿第二定律得:F-μmg=MaB
得:F=28N
(3)撤去水平力F时,A、B的速度为:
vAO=aAt=2m/s
vBO=aBt=4m/s
当A、B速度相等时弹簧的弹性势能最大,根据动量守恒有:
mvAO+MvBO=(m+M)v
得:v=
m/s
所以根据能量守恒定律得:Ep=
m
+
M
-
(m+M)v2=3J
(4)撤去F后,当弹簧恢复原长过程中,A、B动量,能量守恒:
mvAO+MvBO=mvA+MvB
m
+
M
=
m
+
M
所以:vA=5m/s vB=3m/s
之后A做减速运动,B做加速运动,设它们达到共同速度v′
根据动量守恒可知:v′=v=
m/s
由动能定理有:-μmgSA=
mv2-
m
μmgSB=
Mv′2-
M
所以:SA=
mSB=
m
△S=SA-SB=
=0.75m<1m
因此两者不会分离,小物体将停在距C点0.75m处.
答:(1)恒力F作用的这1s内小物体A的加速度为2m/s2,位移为1m.
(2)作用力F的大小是28N;
(3)A压缩弹簧过程中弹簧的最大弹性势能Ep是3J;
(4)小物体不能滑板相分离,小物体将停在距C点0.75m处.
aA=
| μmg |
| m |
则位移为:SA=
| 1 |
| 2 |
| 1 |
| 2 |
(2)这1S内滑板B的位移为:SB=SA+L=1+1=2m
对B有:SB=
| 1 |
| 2 |
得:aB=
| 2SB |
| t2 |
| 2×2 |
| t2 |
根据牛顿第二定律得:F-μmg=MaB
得:F=28N
(3)撤去水平力F时,A、B的速度为:
vAO=aAt=2m/s
vBO=aBt=4m/s
当A、B速度相等时弹簧的弹性势能最大,根据动量守恒有:
mvAO+MvBO=(m+M)v
得:v=
| 7 |
| 2 |
所以根据能量守恒定律得:Ep=
| 1 |
| 2 |
| v | 2 A |
| 1 |
| 2 |
| v | 2 B |
| 1 |
| 2 |
(4)撤去F后,当弹簧恢复原长过程中,A、B动量,能量守恒:
mvAO+MvBO=mvA+MvB
| 1 |
| 2 |
| v | 2 AO |
| 1 |
| 2 |
| v | 2 BO |
| 1 |
| 2 |
| v | 2 A |
| 1 |
| 2 |
| v | 2 B |
所以:vA=5m/s vB=3m/s
之后A做减速运动,B做加速运动,设它们达到共同速度v′
根据动量守恒可知:v′=v=
| 7 |
| 2 |
由动能定理有:-μmgSA=
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 A |
μmgSB=
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 B |
所以:SA=
| 51 |
| 16 |
| 39 |
| 16 |
△S=SA-SB=
| 3 |
| 4 |
因此两者不会分离,小物体将停在距C点0.75m处.
答:(1)恒力F作用的这1s内小物体A的加速度为2m/s2,位移为1m.
(2)作用力F的大小是28N;
(3)A压缩弹簧过程中弹簧的最大弹性势能Ep是3J;
(4)小物体不能滑板相分离,小物体将停在距C点0.75m处.
点评:本题是复杂的力学问题,在分析运动情况的基础上,运用力学基本规律:牛顿第二定律、运动学公式、动量守恒和能量守恒进行求解.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目

 (2008?荆州一模)在水平面上有一个质量为4kg的物体,物体在水平拉力F的作用下由静止开始运动,10s后拉力大小减小为
(2008?荆州一模)在水平面上有一个质量为4kg的物体,物体在水平拉力F的作用下由静止开始运动,10s后拉力大小减小为 (2008?荆州一模)如图所示,A与B质点的运动情况在V-t图象中,由A与B表示,则下述正确的是( )
(2008?荆州一模)如图所示,A与B质点的运动情况在V-t图象中,由A与B表示,则下述正确的是( )