题目内容
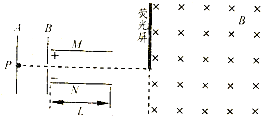 如图所示,位于A板附近的放射源P连续释放出质量分别为m和2m、电荷量均为+q的a、b两种粒子,它们从静止开始经极板A、B间电场加速后,沿中心轴线方向进入平行极板M、N间的偏转电场,飞出偏转电场后进入右侧的有界匀强磁场,最后打在位于磁场边界上的荧光屏上并产生光斑(荧光屏的下端位于中心轴线上).已知A、B问电压为U1;极板M、N长为L,间距为d,也板间电压为U2,磁场的磁感应强度大小为B、方向垂直纸面向里,磁场的左边界与中心轴线垂直.不计粒子的重力及其相互间的作用.求:
如图所示,位于A板附近的放射源P连续释放出质量分别为m和2m、电荷量均为+q的a、b两种粒子,它们从静止开始经极板A、B间电场加速后,沿中心轴线方向进入平行极板M、N间的偏转电场,飞出偏转电场后进入右侧的有界匀强磁场,最后打在位于磁场边界上的荧光屏上并产生光斑(荧光屏的下端位于中心轴线上).已知A、B问电压为U1;极板M、N长为L,间距为d,也板间电压为U2,磁场的磁感应强度大小为B、方向垂直纸面向里,磁场的左边界与中心轴线垂直.不计粒子的重力及其相互间的作用.求:(1)两种粒子射入偏转电场时的初速度;
(2)两种粒子离开偏转电场时的偏转距离和偏转角度θ的正切值;
(3)实验发现,荧光屏上出现了两个光斑,求这两个光斑间的距离.
分析:(1)对两个粒子的直线加速过程分别运用动能定理列式求解即可;
(2)粒子在偏转电场中做类似平抛运动,根据平抛运动的分运动公式列式求解出偏转距离和偏转角度正切值表达式进行讨论即可;
(3)粒子射入磁场后做匀速圆周运动,根据洛伦兹力提供向心力列式求解运动的半径,然后结合几何关系求解两个光斑间的距离.
(2)粒子在偏转电场中做类似平抛运动,根据平抛运动的分运动公式列式求解出偏转距离和偏转角度正切值表达式进行讨论即可;
(3)粒子射入磁场后做匀速圆周运动,根据洛伦兹力提供向心力列式求解运动的半径,然后结合几何关系求解两个光斑间的距离.
解答:解:(1)设a、b粒子射入偏转电场时的初速度分别为v0a和v0b,有:
qU1=
m
解得:
v0a=
根据动能定理,有:
qU1=
?2m
解得:
v0b=
;
(2)设a粒子在偏转电场中的偏转距离为y,偏角为θ,有:
y=
?
?t2
L=v0at
vy=
?t
tanθ=
解得:
y=
;
tanθ=
;
可见偏距和偏角与粒子本身的比荷无关,两种粒子偏距和偏角相同.
(3)对a粒子,射出偏转电场时,设速度为va,有:
va=
粒子射入磁场后,有:
qvaB=m
由几何关系得,粒子在磁场中的射入点与其光斑间的距离为:
Da=2Racosθ
解得:Da=
;
同理可得b粒子在磁场中的射入点与其光斑间的距离为:
Db=
两个光斑间的距离为:
△D=
;
答:(1)a、b两种粒子射入偏转电场时的初速度分别为:
,
;
(2)两种粒子离开偏转电场时的偏转距离和偏转角度θ的正切值为
;
(3)这两个光斑间的距离为
.
qU1=
| 1 |
| 2 |
| v | 2 0a |
解得:
v0a=
|
根据动能定理,有:
qU1=
| 1 |
| 2 |
| v | 2 0b |
解得:
v0b=
|
(2)设a粒子在偏转电场中的偏转距离为y,偏角为θ,有:
y=
| 1 |
| 2 |
| qU2 |
| md |
L=v0at
vy=
| qU2 |
| md |
tanθ=
| vy |
| v0a |
解得:
y=
| U2L2 |
| 4U1d |
tanθ=
| U2L |
| 2U1d |
可见偏距和偏角与粒子本身的比荷无关,两种粒子偏距和偏角相同.
(3)对a粒子,射出偏转电场时,设速度为va,有:
va=
| v0a |
| cosθ |
粒子射入磁场后,有:
qvaB=m
| ||
| Ra |
由几何关系得,粒子在磁场中的射入点与其光斑间的距离为:
Da=2Racosθ
解得:Da=
| 2 |
| B |
|
同理可得b粒子在磁场中的射入点与其光斑间的距离为:
Db=
| 2 |
| B |
|
两个光斑间的距离为:
△D=
2(
| ||
| B |
|
答:(1)a、b两种粒子射入偏转电场时的初速度分别为:
|
|
(2)两种粒子离开偏转电场时的偏转距离和偏转角度θ的正切值为
| U2L |
| 2U1d |
(3)这两个光斑间的距离为
2(
| ||
| B |
|
点评:本题关键是明确粒子的运动规律,然后分直线加速、类似平抛运动和匀速圆周运动三个过程分别选用相应的规律进行分析.

练习册系列答案
相关题目
 偏移距离;
偏移距离;