题目内容
1.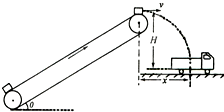 如图是利用传送带装运煤块的示意图.其中传送带长20m,倾角θ=37°,煤块与传送带间的动摩擦因数μ=0.8,传送带的主动轮和从动轮半径相等,主动轮轴顶端与运煤车底板间的竖起高度H=3.2m,与运煤车车箱中心的水平距离x=1.6m.现在传送带底端由静止释放一些煤块(可视为质点),煤块在传送带的作用下先做匀加速直线运动,后与传送带一起做匀速运动,到达主动轮时随轮一起匀速转动.要使煤块在轮的最高点水平抛出并落在车箱中心,取g=10m/s2,sin37°=0.6,cos37°=0.8,求:
如图是利用传送带装运煤块的示意图.其中传送带长20m,倾角θ=37°,煤块与传送带间的动摩擦因数μ=0.8,传送带的主动轮和从动轮半径相等,主动轮轴顶端与运煤车底板间的竖起高度H=3.2m,与运煤车车箱中心的水平距离x=1.6m.现在传送带底端由静止释放一些煤块(可视为质点),煤块在传送带的作用下先做匀加速直线运动,后与传送带一起做匀速运动,到达主动轮时随轮一起匀速转动.要使煤块在轮的最高点水平抛出并落在车箱中心,取g=10m/s2,sin37°=0.6,cos37°=0.8,求:(l)传送带匀速运动的速度v及主动轮和从动轮的半径R
(2)煤块在传送带上由静止开始加速至落到车底板所经过的时间T.
分析 (1)根据平抛运动的高度确定平抛的时间,再根据水平位移求出平抛运动的初速度.平抛运动的初速度等于传送带匀速运动的速度v.
当煤块到达轮的最高点时对轮的压力为零,煤块做平抛运动,根据牛顿第二定律求出从动轮的半径R.
(2)根据牛顿第二定律求出煤块做匀加速直线运动的加速度,根据t=$\frac{v}{a}$求出匀加速运动的时间,然后求出匀速运动的时间,加上平抛运动的时间,三个时间之和为煤块在传送带上由静止开始加速至落到车底板所经过的时间T.
解答 解:(l)煤块离开轮的最高点后做平抛运动,由平抛运动的公式,得:x=vt′,H=$\frac{1}{2}$gt′2
解得:v=x$\sqrt{\frac{g}{2H}}$=1.6×$\sqrt{\frac{10}{2×3.2}}$=2m/s
要使煤块在轮的最高点做平抛运动,则煤块到达轮的最高点时对轮的压力为零,由牛顿第二定律,得:
mg=m$\frac{{v}^{2}}{R}$
代入数据得:R=$\frac{{v}^{2}}{g}$=0.4m
故传送带匀速运动的速度v为2m/s,从动轮的半径R为0.4m.
(2)由牛顿第二定律得:
煤块匀加运动的加速度 a=$\frac{μmgcos37°-mgsin37°}{m}$=μgcos37°-gsin37°=0.8×8-6=0.4m/s2
由v=v0+at得:
匀加速运动的时间 t1=$\frac{v}{a}$=$\frac{2}{0.4}$s=5s
匀加速运动的位移为:x1=$\frac{1}{2}$at12=$\frac{1}{2}$×0.4×25m=5m,
则匀速运动的时间为:t2=$\frac{L-{x}_{1}}{v}$=$\frac{20-5}{2}$s=7.5s,
平抛运动的时间为:t′=$\sqrt{\frac{2H}{g}}$=$\sqrt{\frac{2×3.2}{10}}$s=0.8s,
则煤块在传送带上由静止开始加速至落回运煤车车箱中心所经过的时间为:T=t1+t2+t′=5+7.5+0.8=13.3s.
答:
(1)传送带匀速运动的速度v为2m/s,主动轮和从动轮的半径R为0.4m;
(2)煤块在传送带上由静止开始加速至落回运煤车车箱中心所经过的时间T为13.3s.
点评 解决本题的关键知道平抛运动的初速度等于传送带的速度,以及知道煤块先做匀加速运动再做匀速运动,最后做平抛运动,能边计算边分析物体的运动情况.

| A. | 磁感线是用来形象描绘磁场的假想曲线,不是客观存在的曲线 | |
| B. | 磁感线是磁场中小磁针排列成的曲线或小铁屑排成的曲线 | |
| C. | 磁感线从磁体的N极出发到S极终止 | |
| D. | 磁感线的切线方向表示磁场方向,不表示磁感应强度方向 |
| A. | ${v}_{m}^{2}$<μgs | B. | ${v}_{m}^{2}$>μgs | C. | ${v}_{m}^{2}$<2μgs | D. | ${v}_{m}^{2}$>2μgs |
| A. | 9.8m | B. | 4.9(2n+1)m | C. | 0 | D. | 无法确定 |
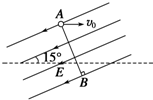 如图所示,真空中的匀强电场与水平方向成15°角,AB直线垂直匀强电场E.现有一质量为m、电荷量为+q的小球在A点以初速度大小为v0方向水平向右抛出,经时间t小球下落到C点(图中未画出)时速度大小仍为v0,则小球由A点运动到C点的过程中,下列说法正确的是( )
如图所示,真空中的匀强电场与水平方向成15°角,AB直线垂直匀强电场E.现有一质量为m、电荷量为+q的小球在A点以初速度大小为v0方向水平向右抛出,经时间t小球下落到C点(图中未画出)时速度大小仍为v0,则小球由A点运动到C点的过程中,下列说法正确的是( )| A. | C点可能位于AB直线的左下侧 | B. | 电场力对小球做功为零 | ||
| C. | 小球的电势能增大 | D. | 小球的机械能一定减小 |
 如图所示,在地面上方等间距分布着足够多的、水平方向的条形匀强磁场,每一条形磁场区域的宽度及相邻区域的间距均为d.现有一边长也为d的正方形线框在离地高h处以水平初速度v0从左侧磁场边缘进入磁场,运动中线框平面始终竖直,最终落在地面上,不计空气阻力,则( )
如图所示,在地面上方等间距分布着足够多的、水平方向的条形匀强磁场,每一条形磁场区域的宽度及相邻区域的间距均为d.现有一边长也为d的正方形线框在离地高h处以水平初速度v0从左侧磁场边缘进入磁场,运动中线框平面始终竖直,最终落在地面上,不计空气阻力,则( )| A. | 线框在空中运动的时间一定为$\sqrt{\frac{2h}{g}}$ | |
| B. | h越大线框运动的水平位移一定越大 | |
| C. | v0的大小连续变化,线框落地点也一定相应的连续变化 | |
| D. | v0越大线框运动过程中产生的焦耳热一定越多 |
| A. | 点电荷是指体积很小的电荷 | |
| B. | 根据F=k$\frac{{q}_{1}{q}_{2}}{{r}^{2}}$知,当两电荷间的距离趋近于零时,静电力将趋于无穷大 | |
| C. | 若两点电荷的电荷量q1>q2,则q1对q2的静电力等于q2对q1的静电力 | |
| D. | 用库仑定律计算出的两电荷间的作用力是两者受力的总和 |
 如图所示,半径R=0.4m的光滑半圆轨道与粗糙的水平面相切于A点,质量为 m=1kg的小物体(可视为质点)在水平拉力的作用下,从C点运动到A点,物体从A点进入半圆轨道的同时撤去外力,物体沿半圆轨道通过最高点B后作平抛运动,正好落在C点,已知AC=2m,g取10m/s2,试求:
如图所示,半径R=0.4m的光滑半圆轨道与粗糙的水平面相切于A点,质量为 m=1kg的小物体(可视为质点)在水平拉力的作用下,从C点运动到A点,物体从A点进入半圆轨道的同时撤去外力,物体沿半圆轨道通过最高点B后作平抛运动,正好落在C点,已知AC=2m,g取10m/s2,试求: 如图,A、B两质点绕同一圆心沿顺时针方向做匀速圆周运动,B的周期分别为T1、T2,且T1<T2,在某一时刻两质点相距最近时开始计时,求:
如图,A、B两质点绕同一圆心沿顺时针方向做匀速圆周运动,B的周期分别为T1、T2,且T1<T2,在某一时刻两质点相距最近时开始计时,求: