题目内容
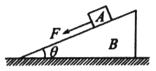
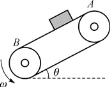
【题目】如图所示,传送带与地面的倾角θ=37°,从A至B的长度x=16 m,传送带以v=10 m/s的速率逆时针转动.在传送带上端A由静止释放一个质量为m=0.5 kg的物体,它与传送带之间的动摩擦因数μ=0.5,则物体从A运动到B所需的时间t是多少?(取g=10 m/s2,sin 37°=0.6,cos 37°=0.8)
【答案】2 s
【解析】
将物体从传送带的A端释放后，物体由静止开始下滑，当下滑速度小于传送带速度时，物体受到的摩擦力沿斜面向下.设物体的加速度为a1，由牛顿第二定律有：
代入数据解得：
；物体加速至与传送带速度相等时需要的时间：
发生的位移：
代入数据解得：
所以物体加速到
时仍未到达B点，此时摩擦力方向改变；设物体的加速度为a2，从速度大于v运动到B的时间为t2，位移为x2，由牛顿第二定律有：
代入数据解得：
；由运动学公式有：
将已知数据代入上式解得t2=1 s，t2=-11 s(舍去)
故物体经历的总时间：
答：物体从A运动到B需时间是2s.
【题目】用对温度敏感的半导体材料制成的某热敏电阻
，在给定温度范围内，其阻值随温度的变化是非线性的．某同学将和两个适当的固定电阻
、
连成图1虚线框内所示的电路，以使该电路的等效电阻
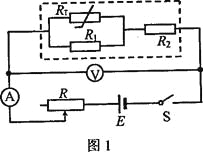
的阻值随所处环境温度的变化近似为线性的，且具有合适的阻值范围．为了验证这个设计，他采用伏安法测量在不同温度下的阻值，测量电路如图1所示，图中的电压表内阻很大．的测量结果如表所示．
．温度t（℃） | 30.0 | 40.0 | 50.0 | 60.0 | 70.0 | 80.0 | 90.0 |
RL阻值（Ω） | 54.3 | 51.5 | 48.3 | 44.7 | 41.4 | 37.9 | 34.7 |
回答下列问题：
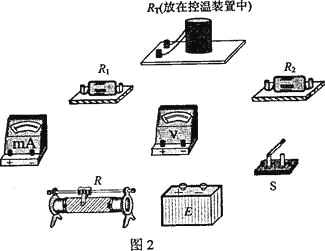
（1）根据图1所示的电路，在图2所示的实物图上连线_______________．
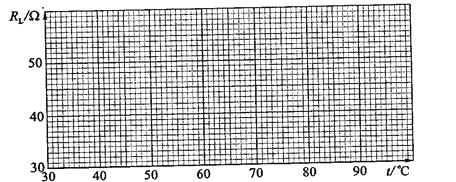
（2）为了检验与f之间近似为线性关系，在坐标纸上作-t关系图线___________．
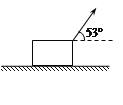
（3）在某一温度下，电路中的电流表、电压表的示数如图3、4所示．电流表的读数为____，电压表的读数为___．此时等效电阻的阻值为___：热敏电阻所处环境的温度约为____．
