题目内容
【题目】如图所示,在半径为R的圆形区域内有匀强磁场,在边长为2R的正方形区域内也有匀强磁场,两个磁场的磁感应强度大小相等,方向都垂直于纸面向里,两个相同的带电粒子以相同的速率分别从M、N两点射入匀强磁场,从M点射入的带电粒子的速度方向指向圆心,从N点射入的带电粒子的速度方向与边界垂直,且N点为正方形的边的中点,则下列说法正确的是( )

A.带电粒子在磁场中飞行的时间可能相同
B.从M点射入的带电粒子可能先飞出磁场
C.从N点射入的带电粒子可能先飞出磁场
D.从N点射入的带电粒子不可能比从M点射入的带电粒子先飞出磁场
【答案】ABD
【解析】
试题分析:带电粒子垂直于磁场方向进入匀强磁场,粒子做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律得:![]() ,解得,粒子的轨道半径:
,解得,粒子的轨道半径:![]() ,两粒子相同、两粒子的速率相同,则两粒子的轨道半径r相同,粒子做圆周运动的周期
,两粒子相同、两粒子的速率相同,则两粒子的轨道半径r相同,粒子做圆周运动的周期![]() 相等,粒子运动轨迹如图所示;
相等,粒子运动轨迹如图所示;
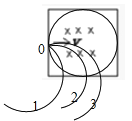
由图示可知,当![]() 时,两粒子在磁场中的运动时间相等,都等于
时,两粒子在磁场中的运动时间相等,都等于![]() ,故A正确;由图示可知,当粒子轨道半径
,故A正确;由图示可知,当粒子轨道半径![]() 时,粒子在圆形磁场中做圆周运动转过的圆心角都小于在正方形区域中做圆周运动转过的圆心角,则粒子在圆形磁场中的运动时间小于在正方形磁场中的运动时间,即从M点射入的粒子运动时间小于从N点射入的粒子运动时间,故BD正确,C错误。
时,粒子在圆形磁场中做圆周运动转过的圆心角都小于在正方形区域中做圆周运动转过的圆心角,则粒子在圆形磁场中的运动时间小于在正方形磁场中的运动时间,即从M点射入的粒子运动时间小于从N点射入的粒子运动时间,故BD正确,C错误。

练习册系列答案
 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目