题目内容
2.甲、乙两车同时从同一地点出发,向同一方向运动,其中甲以8m/s的速度匀速行驶,乙以2m/s2的加速度由静止启动,求:(1)乙车追上甲车前与甲车的最大距离是多少?
(2)乙车经过多长时间追上甲车,此时乙车的速度是多大?
分析 (1)速度相等之前,甲的速度大于乙的速度,两车的距离越来越大,速度相等后,甲车的速度小于乙车的速度,两车的距离越来越小,当两车速度相等时,相距最远.
(2)甲车追上乙车时,两车的位移相等,根据位移关系,运用运动学公式求出追及的时间,根据匀变速直线运动的速度时间公式,求出两车的速度,从而得知两车的速度关系.
解答 解:(1)乙车从静止加速,甲车匀速行驶,所以开始乙车速度小于甲车速度,即υ2<υ1,两车间距离越来越大,随着时间的推移,υ2=υ1之后,乙车速度大于甲车速度υ2>υ1,两车间距离越来越小,因此,当υ2=υ1时,两车间距离最大.
即有:at2=υ1,
解得:t2=$\frac{{v}_{1}}{a}=\frac{8}{2}s=4s$
故经过4s两车相距最远,最远距离为:S=v1t2-$\frac{1}{2}a{t}^{2}$=8×4-$\frac{1}{2}×2×{4}^{2}$=16(m)
(2)甲乙两车同时从同一地点出发,向同一方向运动,乙车追上甲车时,二者位移相同,设甲车位移S1,乙车位移S2
则 S1=S2
即υ1t1=$\frac{1}{2}{at}_{1}^{2}$
解得:t1=$\frac{2{v}_{1}}{a}=\frac{2×8}{2}s=8s$
乙的速度为:υ2=at1=2×8m/s=16m/s
答:(1)乙车追上甲车前与甲车的最大距离是16m
(2)乙车经过多长时间追上甲车,此时乙车的速度是16m/s
点评 该问题为运动学中的追及问题,关键要研究两个物体之间的关系,抓住相遇时位移相等求出运动时间,知道两车速度相等时,两车间距最大.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
12.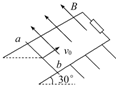 一质量为m、电阻为r的金属杆ab,以一定的初速度v0从一光滑平行金属导轨底端向上滑行,导轨平面与水平面成30°角,两导轨上端用一电阻R相连,如图所示,磁场垂直斜面向上,导轨的电阻不计,金属杆向上滑行到某一高度之后又返回到底端时的速度大小为v,则( )
一质量为m、电阻为r的金属杆ab,以一定的初速度v0从一光滑平行金属导轨底端向上滑行,导轨平面与水平面成30°角,两导轨上端用一电阻R相连,如图所示,磁场垂直斜面向上,导轨的电阻不计,金属杆向上滑行到某一高度之后又返回到底端时的速度大小为v,则( )
 一质量为m、电阻为r的金属杆ab,以一定的初速度v0从一光滑平行金属导轨底端向上滑行,导轨平面与水平面成30°角,两导轨上端用一电阻R相连,如图所示,磁场垂直斜面向上,导轨的电阻不计,金属杆向上滑行到某一高度之后又返回到底端时的速度大小为v,则( )
一质量为m、电阻为r的金属杆ab,以一定的初速度v0从一光滑平行金属导轨底端向上滑行,导轨平面与水平面成30°角,两导轨上端用一电阻R相连,如图所示,磁场垂直斜面向上,导轨的电阻不计,金属杆向上滑行到某一高度之后又返回到底端时的速度大小为v,则( )| A. | 向上滑行的时间大于向下滑行的时间 | |
| B. | 在向上滑行时电阻R上产生的热量小于向下滑行时电阻R上产生的热量 | |
| C. | 向上滑行时与向下滑行时通过电阻R的电荷量相等 | |
| D. | 金属杆从开始上滑至返回出发点,电阻R上产生的热量为$\frac{1}{2}$m(v02-v2) |
13.在匀强磁场中,一矩形金属线框绕与磁感线垂直的转动轴匀速转动,如图甲所示.产生的交变电动势随时间变化的规律如图乙所示.则下列说法正确的是( )


| A. | t=0.01s时穿过线框的磁通量最大 | |
| B. | 该交变电动势的有效值为11$\sqrt{2}$V | |
| C. | 该交变电动势的瞬时值表达式为e=22$\sqrt{2}$sinV | |
| D. | 电动势瞬时值为22V时,线圈平面与中性面的夹角为45° |
17.一个质点做变速直线运动的v-t图象如图所示,下列说法中正确的是( )


| A. | 第1 s内与第5 s内的速度方向相同 | |
| B. | 第1 s内的加速度大小大于第5 s内的加速度 | |
| C. | OA、AB、BC段的加速度大小关系是aBC>aOA>aAB | |
| D. | OA段的加速度与速度方向相同,BC段的加速度与速度方向相反 |
14.一个物体做变速直线运动,物体的加速度从某一值逐渐减小到零.则在此过程中,关于该物体的运动情况,下列可能的是( )
| A. | 物体速度不断增大,加速度减小到零时,物体速度最大 | |
| B. | 物体速度不断减小,加速度减小到零时,物体速度为零 | |
| C. | 物体速度不断减小到零,然后物体反向做加速直线运动 | |
| D. | 物体先做匀减速直线运动,然后物体反向做匀加速直线运动 |
4.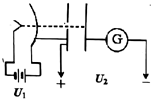 如图所示的装置中,左边的非匀强电场使电子加速,右边的匀强电场使电子减速,设非匀强电场的电压为U1,匀强电场的电压为U2.现在让初速度为零的电子从左边进入(电子的重力不计),则( )
如图所示的装置中,左边的非匀强电场使电子加速,右边的匀强电场使电子减速,设非匀强电场的电压为U1,匀强电场的电压为U2.现在让初速度为零的电子从左边进入(电子的重力不计),则( )
 如图所示的装置中,左边的非匀强电场使电子加速,右边的匀强电场使电子减速,设非匀强电场的电压为U1,匀强电场的电压为U2.现在让初速度为零的电子从左边进入(电子的重力不计),则( )
如图所示的装置中,左边的非匀强电场使电子加速,右边的匀强电场使电子减速,设非匀强电场的电压为U1,匀强电场的电压为U2.现在让初速度为零的电子从左边进入(电子的重力不计),则( )| A. | 若电流计的指针未偏转,则U2<U1 | |
| B. | 若电流计的指针未偏转,则U2>U1 | |
| C. | 在U1电场中,电子的电势能增加,动能减少 | |
| D. | 在U2电场中,电子的电势能增加,动能减少 |
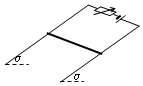 如图所示,光滑导轨与水平面成α角,导轨宽L,匀强磁场磁感应强度为B,金属杆长也为L,质量为m,水平放在导轨上.当回路总电流为I1时,金属杆正好能静止.求:
如图所示,光滑导轨与水平面成α角,导轨宽L,匀强磁场磁感应强度为B,金属杆长也为L,质量为m,水平放在导轨上.当回路总电流为I1时,金属杆正好能静止.求: 如图所示,带电小球A和B放在倾角为30°的光滑绝缘斜面上,质量均为m,所带电荷量分别为+q和-q,沿斜面向上的恒力F作用于A球,可使A、B保持间距r不变沿斜面向上加速运动,已知重力加速度为g,静电力常量k,求:
如图所示,带电小球A和B放在倾角为30°的光滑绝缘斜面上,质量均为m,所带电荷量分别为+q和-q,沿斜面向上的恒力F作用于A球,可使A、B保持间距r不变沿斜面向上加速运动,已知重力加速度为g,静电力常量k,求: