Question

如图6-3-25所示，在倾角θ=37°的绝缘斜面所在空间存在着竖直向上的匀强电场，场强E=4.0×10³ N/C，在斜面底端有一与斜面垂直的绝缘弹性挡板.质量m=0.20 kg的带电滑块从斜面顶端由静止开始滑下，滑到斜面底端与挡板相碰后以碰前的速率返回.已知斜面的高度h=0.24 m，滑块与斜面间的动摩擦因数μ=0.30，滑块带电荷q=-5.0×10^-4 C.取重力加速度g=10 m/s²，sin37°=0.60，cos37°=0.80.求：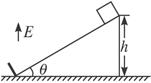

图6-3-25

（1）滑块从斜面最高点滑到斜面底端时的速度大小；

（2）滑块被挡板弹回能够沿斜面上升的最大高度.

Answer 1

解析：（1）滑块沿斜面滑下的过程中，受到的滑动摩擦力f=μ(mg+qE)cos37°

设到达斜面底端时的速度为v₁，根据定理

（mg+qE）h-f=mv₁²

解得v₁=2.4 m/s.

（2）滑块第一次与挡板碰撞后沿斜面返回上升的高度最大，设此高度为h₁，根据动能定理：

-(mg+qE)h₁-f=-mv₁²

代入数据解得h₁=0.10 m.

答案：（1）v₁=2.4 m/s  （2）h₁=0.10 m