Question

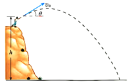
【题目】如图所示，绝缘水平传送带长L1=3.2m，以恒定速度v=4m/s顺时针转动，传送带右侧与光滑平行金属导轨平滑连接，导轨与水平面夹角α=370，导轨长L2=16m、间距d=0.5m，底端接有R=3Ω的电阻，导轨区域内有垂直轨道平面向下、B=2T的匀强磁场．一质量m=0.5kg、长度为d=0.5m、电阻r=1Ω的金属杆无初速度地放于传送带的左端，在传送带作用下向右运动，到达右端时能平滑地滑上金属轨道，整个过程中杆始终与运动方向垂直，且杆与轨道接触良好，到达轨道底端时已开始做匀速运动．已知杆与传送带间动摩擦因数μ=0.5，导轨电阻忽略不计，g取10m/ s2（sin37°=0.6，cos37°=0.8）．求：

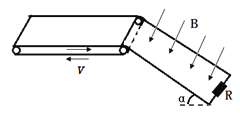
（1）杆在水平传送带上的运动时间；

（2）杆刚进入倾斜金属导轨时的加速度；

（3）杆下滑至底端的过程中电阻R中产生的焦耳热.

Answer 1

【答案】（1）1.2s；（2）；方向沿轨道斜面向下（3）12J

【解析】

（1）杆在传送带上加速运动时

加速运动的时间

这段时间内的位移

因，此后杆匀速运动

故，杆在水平传送带上的运动时间

（2）杆刚进入磁场

由牛顿第二定律

代入数据解得：，方向沿轨道斜面向下

（3）杆在轨道上匀速运动时有

解得

下滑过程中，闭合回路中产生的总焦耳热

电阻R中产生的焦耳热

代入数据解得