��Ŀ����
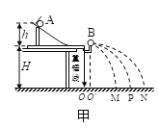
����Ŀ������ΪM��ƽ�峵P��h������Ϊm��С���Q�Ĵ�С���ƣ�λ��ƽ�峵����ˣ�ϵͳԭ����ֹ�ڹ⻬ˮƽ������ϣ�һ�����쳤������ϸ����ΪR��һ������Q���Ϸ���ΪR������һ��ϵһ����ҲΪm��С��С����)����С��������������ֱλ�ó�![]() �ǣ��ɾ�ֹ�ͷţ�С����͵�ʱ��Q����ײʱ�伫�̣�����������ʧ����֪Q�뿪ƽ�峵ʱ�ٶȴ�С��ƽ�峵�ٶȵ�������Q��P֮��Ķ�Ħ������Ϊ
�ǣ��ɾ�ֹ�ͷţ�С����͵�ʱ��Q����ײʱ�伫�̣�����������ʧ����֪Q�뿪ƽ�峵ʱ�ٶȴ�С��ƽ�峵�ٶȵ�������Q��P֮��Ķ�Ħ������Ϊ![]() ��M��m=4��1���������ٶ�Ϊg����
��M��m=4��1���������ٶ�Ϊg����
��1��С��鵽����͵���Q��ײ֮ǰ˲����ٶ��Ƕ��
��2��С���Q�뿪ƽ�峵ʱƽ�峵���ٶ�Ϊ���
��3��ƽ�峵P�ij���Ϊ���٣�
��4��С���Q���ʱ��С���ˮƽ����Ϊ���٣�

���𰸡���1��![]() ����2��
����2��![]() ����3��
����3��![]() ����4��
����4��![]()
��������
��1��С���ɾ�ֹ�ڵ���͵�Ĺ����У���е���غ㣬���У�
![]()
���С��鵽����͵���Q��ײ֮ǰ˲����ٶ��ǣ�
![]()
��2��С�������Q��ײʱ��û��������ʧ�����㶯���غ㣬��е���غ㣬��֪��
mv0=mv1+mvQ
![]()
��������ʽ��֪���߽����ٶȣ�
v1=0��![]()
С���Q��ƽ�峵�ϻ��еĹ����У����㶯���غ㣬���У�
mvQ=Mv+m2v
��֪M��m=4��1
![]()
��С���Q�뿪ƽ�峵ʱƽ�峵���ٶ�Ϊ![]() ��
��
��3��С���Q��ƽ�峵P�ϻ����Ĺ����У����ֶ���ת��Ϊ���ܣ����ܵ�ת�����غ㶨�ɣ�֪��
![]()
���ƽ�峵P�ij���Ϊ��
![]()
��4��С���Q��ƽ�峵�ϻ��еĹ����У���ƽ�峵ǰ������ΪLM����ƽ�峵�ɶ��ܶ����ã�
![]()
��ã�
![]()
С���Q�뿪ƽ�峵��ƽ���˶�����ֱ�����У�
![]()
ˮƽ�����У�
x=2vt
��ã�
![]()
С���Q���ʱ��С���ˮƽ���룺
![]()