题目内容
【题目】如图所示,放在粗糙的固定斜面上的物块A和悬挂的物体B均处于静止状态.轻绳AO绕过光滑的定滑轮与轻弹簧的右端及轻绳BO的上端连接于O点,轻弹簧中轴线沿水平方向,轻绳的OC段与竖直方向的夹角θ=53°,斜面倾角α=37°,物块A和B的质量分别为mA=5kg,mB=1.5kg,弹簧的劲度系数k=500N/m,(sin37°=0.6,cos37°=0.8,重力加速度g=10m/s2),求: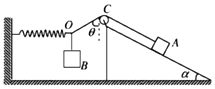
(1)弹簧的伸长量x;
(2)物块A受到的摩擦力.
【答案】
(1)解:对结点O受力分析如图所示:
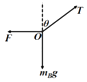
根据平衡条件,有:
Tcosθ﹣mBg=0,
Tsinθ﹣F=0,
且:F=kx,
解得:x=4cm;
(2)解:设物体A所受摩擦力沿斜面向下,对物体A做受力分析如图所示:
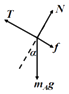
根据平衡条件,有:T﹣f﹣mBgsinα=0,
解得:f=﹣5N,
即物体A所受摩擦力大小为5N,方向沿斜面向上.
【解析】(1)以轻绳OB和物块B为研究对象,受力如图并正交分解,根据平衡条件结合胡克定律求解;(2)对物块A受力如图并正交分解,根据平衡条件列式求解即可.

练习册系列答案
相关题目