题目内容
假设地球的卫星1和月球的卫星2，分别绕地球和月球做匀速圆周运动，如图所示，两颗卫星2的轨道半径相同。已知地球的质量大于月球的质量，两颗卫星相比较，下列说法中正确的是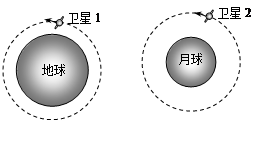
| A．卫星1的向心加速度较小 |
| B．卫星1的动能较大 |
| C．卫星1的周期较小 |
| D．若卫星1是地球的同步卫星，则它的质量一定 |
：C
解析试题分析：根据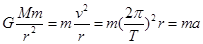
可知
，可知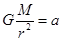卫星1的向心加速度较大；
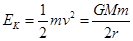，由于卫星的质量不确定，所以不能比较两颗卫星的动能大小；
，所以卫星1的周期较小；若卫星1是地球的同步卫星，则它的质量是不一定的。选项C正确。
考点：万有引力定律及人造卫星。
学练快车道快乐假期暑假作业新疆人民出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 如图所示，a为放在赤道上相对地球静止的物体，随地球自转做匀速圆周运动，b为沿地球表面附近做匀速圆周运动的人造卫星（轨道半径等于地球半径），c为地球的同步卫星，以下关于a、b、c的说法中正确的是（ ）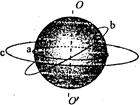
| A．a、b、c做匀速圆周运动的向心加速度大小关系为ab>ac>aa |
| B．b与c相比，b的发射速度大，运行速度vb大 |
| C．a、b、c做匀速圆周运动的线速度大小关系为va=vb>vc |
| D．a、b、c做匀速圆周运动的周期关系为Ta>Tc>Tb |
若已知月球绕地球运动可近似看做匀速圆周运动，并且已知月球绕地球运动的轨道半径r，它绕地球运动的周期T，万有引力常量是G，由此可以知道
A．月球的质量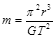 | B．地球的质量 |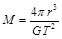
C．月球的平均密度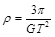 | D．地球的平均密度 |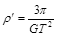
设想我国宇航员随“嫦娥”号登月飞船贴近月球表面做匀速圆周运动，宇航员测出飞船绕行n圈所用的时间为t。登月后，宇航员利用身边的弹簧秤测出质量为m的物体重力G1。已知引力常量为G，根据以上信息可得到
| A．月球的密度 |
| B．飞船的质量 |
| C．月球的第一宇宙速度 |
| D．月球的自转周期 |
某人造卫星绕地球做匀速圆周运动，设地球半径为R，地面重力加速度为g。下列说法正确的( )
A．人造卫星的最小周期为 |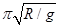
B．卫星在距地面高度R处的绕行速度为 |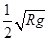
C．卫星在距地面高度R处的加速度为 |
| D．地球同步卫星的速率比近地卫星的速率小，所以发射同步卫星所需的能量较小 |
物体在万有引力场中具有的势能叫做引力势能.若取两物体相距无穷远时的引力势能为零，则一个质量为m0的质点到质量为M0的引力源中心的距离为r0时，其万有引力势能为EP＝－
（式中G为万有引力常量）.一颗质量为m的人造地球卫星沿轨道半径为r1的圆形轨道环绕地球做匀速圆周运动，已知地球的质量为M，要使此卫星绕地球做匀速圆周运动的轨道半径增大为r2，则卫星上的发动机所消耗的最小能量为：（假设卫星的质量始终不变，不计一切阻力及其它星体的影响）
A．E＝ ( － ) | B．E＝GMm(－) |
C．E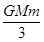＝ (－) | D．E＝ (－) |
不久前欧洲天文学家在太阳系外发现了一颗可能适合人类居住的行星，该行星的质量是 地球质量的5倍，直径是地球直径的1.5倍。设想在该行星表面附近绕行星沿圆轨道运 行的人造卫星的动能为Ek1，在地球表面附近绕地球沿圆轨道运行的相同质量的人造卫 星的动能为Ek2，则Ek1:Ek2为
| A．7.5 | B．3.33 | C．0.3 | D．0.13 |
两质量之比为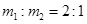
的卫星绕地球做匀速圆周运动，运动的轨道半径之比
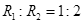，则下列关于两颗卫星的说法中正确的是
A．线速度大小之比为 |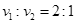
B．向心加速度大小之比为 |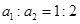
C．运动的周期之比为 |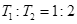
D．动能之比为 |
