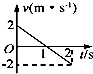题目内容
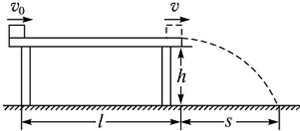
9. 如图所示,小滑块在较长的斜面顶端,以初速度v0=2m/s、加速度a=2m/s2沿斜面向下加速滑动,在到达底端的前1s内,所滑过的距离为7m,则:
如图所示,小滑块在较长的斜面顶端,以初速度v0=2m/s、加速度a=2m/s2沿斜面向下加速滑动,在到达底端的前1s内,所滑过的距离为7m,则:(1)小球在斜面上滑行的时间为多少?
(2)小球到达斜面底端时的速度v是多少?
(3)斜面的长度是多少?
分析 (1、2)根据匀变速直线运动的位移时间公式得出最后1s内的初速度,结合速度时间公式求出小球到达底端的速度.根据速度时间公式求出小球在斜面上滑行的时间.
(3)根据平均速度推论求出斜面的长度.
解答 解:(1、2)到达底端的前1s内,所滑过的距离为7m,根据$x′=v′t′+\frac{1}{2}at{′}^{2}$得最后1s内的初速度为:
$v′=\frac{x′-\frac{1}{2}at{′}^{2}}{t′}=\frac{7-\frac{1}{2}×2×1}{1}m/s=6m/s$,
则到达底端的速度为:
v=v′+at′=6+2×1m/s=8m/s.
可知小球在斜面上滑行的时间为:
$t=\frac{v-{v}_{0}}{a}=\frac{8-2}{2}s=3s$.
(3)根据平均速度推论知,斜面的长度为:
L=$\frac{{v}_{0}+v}{2}t$=$\frac{2+8}{2}×3m=15m$.
答:(1)小球在斜面上滑行的时间为3s;
(2)小球到达斜面底端时的速度v是8m/s;
(3)斜面的长度是15m.
点评 解决本题的关键掌握匀变速直线运动的运动学公式和推论,并能灵活运用,有时运用推论求解会使问题更加简捷.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
20.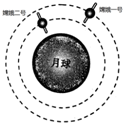 “嫦娥二号”环月飞行的高度为100km,所探测到的有关月球的数据比环月飞行高度为200km的“嫦娥一号”更加翔实.若两颗卫星环月的运行均可视为匀速圆周运动,运行轨道如图所示.则下列说法正确的是( )
“嫦娥二号”环月飞行的高度为100km,所探测到的有关月球的数据比环月飞行高度为200km的“嫦娥一号”更加翔实.若两颗卫星环月的运行均可视为匀速圆周运动,运行轨道如图所示.则下列说法正确的是( )
 “嫦娥二号”环月飞行的高度为100km,所探测到的有关月球的数据比环月飞行高度为200km的“嫦娥一号”更加翔实.若两颗卫星环月的运行均可视为匀速圆周运动,运行轨道如图所示.则下列说法正确的是( )
“嫦娥二号”环月飞行的高度为100km,所探测到的有关月球的数据比环月飞行高度为200km的“嫦娥一号”更加翔实.若两颗卫星环月的运行均可视为匀速圆周运动,运行轨道如图所示.则下列说法正确的是( )| A. | “嫦娥一号”的线速度是“嫦娥二号”的$\frac{\sqrt{2}}{2}$ | |
| B. | “嫦娥一号”的向心加速度是“嫦娥二号”的$\frac{1}{4}$ | |
| C. | 若两者的绕行方向均为逆时针,从图示位置开始,“嫦娥一号”将会从后面追上“嫦娥二号” | |
| D. | 虽然“嫦娥一号”离月球较远,但运行时的向心力可能比“嫦娥二号”大 |
17.如图所示,两个带电球,大球的电荷量大于小球的电荷量,可以肯定( )
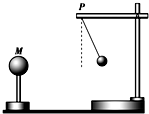

| A. | 两球可能都带正电 | |
| B. | 两球都带负电 | |
| C. | 大球受到的静电力大于小球受到的静电力 | |
| D. | 两球受到的静电力大小相等 |
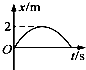
4.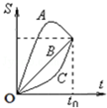 A、B、C三个物体从同一点出发,沿着一条直线运动的位移-时间(S-t)图象如图所示,下列说法中正确的是( )
A、B、C三个物体从同一点出发,沿着一条直线运动的位移-时间(S-t)图象如图所示,下列说法中正确的是( )
 A、B、C三个物体从同一点出发,沿着一条直线运动的位移-时间(S-t)图象如图所示,下列说法中正确的是( )
A、B、C三个物体从同一点出发,沿着一条直线运动的位移-时间(S-t)图象如图所示,下列说法中正确的是( )| A. | 三者者的位移不相等 | |
| B. | A物体做曲线运动 | |
| C. | 三个物体在0~t0时间内的平均速度vA>vC>vB | |
| D. | 三个物体在0~t0时间内的平均速度vA=vB=vC |
1.如图所示为在同一直线上运动的A、B两质点的x-t图象.由图可知( )
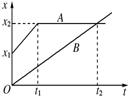

| A. | B在t2时刻追上A,并在此后跑在A的前面 | |
| B. | t=0时,A在B的后面 | |
| C. | B开始运动的速度比A小,t2时刻后才大于A的速度 | |
| D. | A运动的速度始终比B大 |
19.下列关于民间俗语所说的时间,理解错误的是( )
| A. | 表示做事得过且过说“做一天和尚撞一天钟”“一天”指时间间隔 | |
| B. | 形容做事没有持久性说“三分钟”热度,“三分钟”指时刻 | |
| C. | 形容事情不是一蹴而就时说“冰冻三尺非一日之寒”“一日”指时刻 | |
| D. | 进行交通安全教育时说“宁停三分,不抢一秒”“三分”“一秒”均指时刻 |