题目内容
【题目】功是物理学中非常重要的概念,通过做功的过程可以实现能量转化。
(1)一直流电动机,线圈电阻R=2.0Ω,当它两端所加的电压U=24V时,电动机正常运转,测得通过其电流I=0.50A。求此工作状态下,这台电动机将电能转化为机械能的效率是多少?(保留三位有效数字)
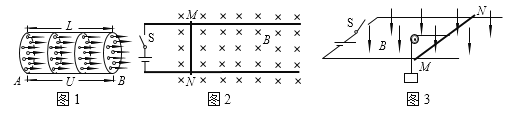
(2)在电路中电能转化为其他形式能的过程就是电流做功的过程,电流做功的过程本质上是导体中恒定电场的电场力对定向移动的自由电荷做功的过程。由同种材料制成的很长的圆柱形实心金属导体,在其上选取长为L的导体做为研究对象,如图1所示,当其两端的电势差恒为U时,形成的恒定电流的大小为I,即相同时间内通过导体A端橫截面的电荷量与通过B端的电荷量相等,也就等于通过这段导体的电荷量。设导体中的恒定电场为匀强电场,自由电子的电荷量为e,它们定向移动的速率恒定且均相同。
①求每个自由电子在导体中做定向移动的平均阻力f;
②结合电流的定义式I=![]() ,从恒定电场的电场力对自由电子做功的角度,证明电流通过这段金属导体做功的功率为P=UI;
,从恒定电场的电场力对自由电子做功的角度,证明电流通过这段金属导体做功的功率为P=UI;
③结合电流的定义式I=![]() ,从恒定电场的电场力对自由电子做功的角度,证明电流通过这段金属导体在时间t内产生的焦耳热为Q=UIt;
,从恒定电场的电场力对自由电子做功的角度,证明电流通过这段金属导体在时间t内产生的焦耳热为Q=UIt;
(3)如图2所示为简化的直流电动机模型,固定于水平面的两根平行金属导轨,处于竖直向下的匀强磁场中,在两导轨的左端通过开关连接一电源。一根导体棒MN放置在导轨上,导体棒与导轨间的阻力恒定且不为0。闭合开关S后,导体棒由静止开始运动,运动过程中切割磁感线产生动生电动势,该电动势总要削弱电源电动势的作用,我们把这个电动势称为反电动势E反。若导体棒运动过程中始终与导轨垂直且接触良好,此“电动机模型”稳定运行时通过导体棒的电流为I。请证明此“电动机模型”稳定运行时的机械功率为P机=IE反;
(4)如图3所示为简化的直流电动机模型,固定于水平面的两根平行金属导轨,处于竖直向下的匀强磁场中,在两导轨的左端通过开关连接一电源。一根导体棒MN放置在导轨上,导体棒用通过定滑轮的轻细线与重物相连。闭合开关S后,导体棒由静止开始运动,运动过程中切割磁感线产生动生电动势,该电动势总要削弱电源电动势的作用,我们把这个电动势称为反电动势E反。若导体棒运动过程中始终与导轨垂直且接触良好,且一切摩擦均可忽略不计,此“电动机模型”稳定运行时通过导体棒的电流为I。请证明此“电动机模型”稳定运行时对重力做功的功率为P=IE反。
【答案】(1)95.8%;(2)①![]() ;②证明见解析;③证明见解析;(3)证明见解析;(4)证明见解析
;②证明见解析;③证明见解析;(3)证明见解析;(4)证明见解析
【解析】
(1)电动机的输入功率
![]()
产生热的功率
![]()
因此输出机械能的功率
![]()
电能转化为机械能的效率为
![]()
(2)①因自由电子做匀速运动,因此有
![]()
②导体内恒定电场的电场力对通过这段导体的一个自由电子所做的功
![]()
设t时间内共有n个自由电子通过这段导体,则恒定电场的电场力对自由电子所做的总功
![]()
因导体中的电流
I=![]() =
=![]()
所以可得
W=UIt
因此电流通过这段金属导体做功的功率为
![]()
③恒定电流中自由电子定向移动的速度保持不变,即自由电子的定向移动的动能不变,根据功能关系可知,电场力所做的功等于阻力做的功,觅阻力做的功等于电流通过导体产生的焦耳热,因此
Q=W电=UIt
(3)“电动机模型”稳定运行时的机械功率就是安培力做功的功率。设稳定运行时导体棒的速度为v,则
P机=F安v=BILv
又因
E反=BLv
所以
P机=E反I
(4) “电动机模型”稳定运行时,导体棒受力分析可知
![]()
因此克服重力做功的机械功率就是安培力做功的功率。设稳定运行时导体棒的速度为v,则
P机=F安v=BILv
又因
E反=BLv
所以
P机=IE反
即
![]()

 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案