题目内容
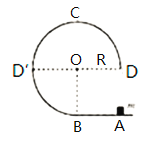
【题目】如图所示,质量![]() 的小车以
的小车以![]() 的速度在光滑的水平面上向左运动,小车上表面的
的速度在光滑的水平面上向左运动,小车上表面的![]() 部分是粗糙的水平轨道,
部分是粗糙的水平轨道,![]() 部分是光滑的
部分是光滑的![]() 圆弧轨道,圆弧轨道在
圆弧轨道,圆弧轨道在![]() 点的切线水平,整个轨道都是由绝缘材料制成的。小车所在空间内存在方向竖直向上的匀强电场和方向垂直纸面向里的匀强磁场,电场强度大小
点的切线水平,整个轨道都是由绝缘材料制成的。小车所在空间内存在方向竖直向上的匀强电场和方向垂直纸面向里的匀强磁场,电场强度大小![]() ,磁感应强度大小
,磁感应强度大小![]() 。现有一质量
。现有一质量![]() 、带电荷量
、带电荷量![]() 的滑块以
的滑块以![]() 的速度从小车上表面的左端向右运动,当滑块运动到
的速度从小车上表面的左端向右运动,当滑块运动到![]() 点时,其相对地面的速度大小
点时,其相对地面的速度大小![]() ,方向水平向右。已知滑块可视为质点,重力加速度
,方向水平向右。已知滑块可视为质点,重力加速度![]() 取
取![]() 。
。
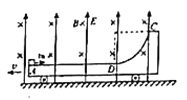
(1)在滑块从![]() 点运动到
点运动到![]() 点的过程中,求小车与滑块组成的系统损失的机械能。
点的过程中,求小车与滑块组成的系统损失的机械能。
(2)当滑块通过![]() 点时,立即撤去磁场,要使滑块不冲出圆弧轨道,求此圆弧轨道的最小半径。
点时,立即撤去磁场,要使滑块不冲出圆弧轨道,求此圆弧轨道的最小半径。
【答案】(1)85J(2)0.71m
【解析】
(1)设滑块运动到D点时的速度大小为v1,小车在此时的速度大小为v2,滑块从A运动到D的过程中系统动量守恒,以向右为正方向,有:mv0-Mv=mv1+Mv2
代入数据解得v2=0
则小车跟滑块组成的系统的初机械能![]()
小车跟滑块组成的系统的末机械能![]()
代入数据解得:E1=110J,E2=25J
小车与滑块组成的系统损失的机械能△E=E1-E2
代入数据解得:△E=85J
(2)设滑块沿圆弧轨道上升到最大高度时,滑块与小车具有共同的速度v3
则由动量守恒定律可得mv1=(M+m)v3
代入数据解得:v3=![]() m/s
m/s
设圆弧轨道的最小半径为R,则由能量守恒关系有:![]()
代入数据解得:R=0.71m

练习册系列答案
相关题目