题目内容
【题目】如图所示,光滑绝缘细杆竖直放置,细杆右侧距杆0.3m处有一固定的正点电荷Q,A、B是细杆上的两点,点A与Q、点B与Q的连线与杆的夹角均为![]() 。一中间有小孔的带电小球穿在绝缘细杆上滑下,通过A点时加速度为零,速度为3m/s,取g=10m/s2。求:
。一中间有小孔的带电小球穿在绝缘细杆上滑下,通过A点时加速度为零,速度为3m/s,取g=10m/s2。求:

(1) 小球下落到B点时的加速度
(2) 小球下落到B点时的速度的大小。
【答案】(1)小球下落到B点时的加速度是20m/s2,方向竖直向下.(2)小球下落到B点时的速度的大小是5m/s.
【解析】
(1)分析小球在A处和B处的受力情况,根据库仑定律和牛顿第二定律分别列式,联立求解小球下落到B点时的加速度;
(2)小球从A到B,电场力做功为零,重力做功为mghAB,根据动能定理求解小球下落到B点时的速度的大小。
(1) 在A处,小球受力如图所示,
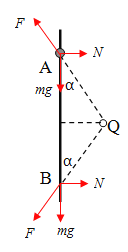
由题意可知
![]()
在B处,小球受力如图所示,根据牛顿第二定律得
![]()
联立以上两式解得:![]() ,方向竖直向下;
,方向竖直向下;
(2) A、B两点位于同一等势面上,所以小球从A运动到B过程中,电场力做功为零,由动能定理得:
![]()
由题,hAB=2×0.3cot37°=0.8m
联立上两式得 vB=5m/s.。

练习册系列答案
相关题目