题目内容
平行金属板M、N间距离为d。其上有一内壁光滑的半径为R的绝缘圆筒与N板相切，切点处有一小孔S。圆筒内有垂直圆筒截面方向的匀强磁场，磁感应强度为B。M板内侧中点处有一质量为m,电荷量为e的静止电子，经过M、N间电压为U的电场加速后射入圆筒，在圆筒壁上碰撞n次后，恰好沿原路返回到出发点。（不考虑重力，设碰撞过程中无动能损失）求：
（1）电子到达小孔S时的速度大小；
（2）电子第一次到达S所需要的时间；
（3）电子第一次返回出发点所需的时间。
解：(1)设加速后获得的速度为v，根据eU=
mv2,得
v=
(2)设电子从M到N所需时间为t1,
则d=
at12=
×
t12
得t1=d
。
(3)电子在磁场做圆周运动的周期为T0=
电子在圆筒内经过n次碰撞回到S，每段圆弧对应的圆心角θ1=π-
n次碰撞对应的总圆心角θ=(n+1)θ1=(n+1)π-2π=(n-1)π
在磁场内运动的时间为t2,t2=
T0=
=
t=2t1+t2=2d
(n=1,2,3,…)
练习册系列答案
相关题目
（2011?自贡模拟）如图所示，半径为r圆心为0的虚线所围的圆形区域内存在垂直纸面向外的匀强磁场，在磁场右侧有一竖直放置的平行金属板M和N，两板间距离为在MN板中央各有一个小孔02、O3，O1，O2，O3在同一水平直线上，与平行金属板相接的是两条竖直放置间距为L的足够长的光滑金属导轨，导体棒PQ与导轨接触良好，与阻值为R的电阻形成闭合回路．（导轨与导体棒的电阻不计），该回路处在磁感应强度大小为B，方向垂直纸面向里的匀强磁场中，整个装置处在真空室中，有一束电荷量为+q、质量为m的粒子流（重力不计），以速率V0从圆形磁场边界上的最低点E沿半径方向射入圆形磁场区域，最后从小孔O3射出．现释放导体棒PQ，其下滑h后开始匀速运动，此后粒子恰好不能从O3射出，而是从圆形磁场的最高点F射出．求：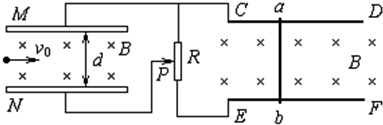
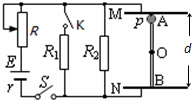如图所示，电源电动势E=50V，内阻r=1Ω，R1=3Ω，R2=6Ω．间距d=0.2m的两平行金属板M、N水平放置，闭合开关S，板间电场视为匀强电场．板间竖直放置一根长也为d的光滑绝缘细杆AB，有一个穿过细杆的带电小球p，质量为m=0.01kg、带电量大小为q=1×10-3C（可视为点电荷，不影响电场的分布）．现调节滑动变阻器R，使小球恰能静止在A处；然后再闭合K，待电场重新稳定后释放小球p．取重力加速度g=10m/s2．求：
如图两块平行金属板M、N竖直放置，两板间电势差U=1.5×103V．现将质量m=1×10-2kg、电荷量q=4×10-5C的带电小球从两板上方的A点以v0=4m/s的初速度水平抛出，小球恰好能从M板上端进入两板之间，并沿直线运动打到N板上的B点．已知A距两板上端的高度为h=0.2m，不计空气阻力，g=10m/s2．则（ ）