题目内容
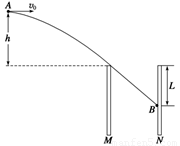
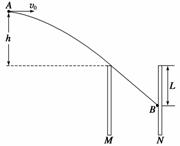
 如图两块平行金属板M、N竖直放置,两板间电势差U=1.5×103V.现将质量m=1×10-2kg、电荷量q=4×10-5C的带电小球从两板上方的A点以v0=4m/s的初速度水平抛出,小球恰好能从M板上端进入两板之间,并沿直线运动打到N板上的B点.已知A距两板上端的高度为h=0.2m,不计空气阻力,g=10m/s2.则( )
如图两块平行金属板M、N竖直放置,两板间电势差U=1.5×103V.现将质量m=1×10-2kg、电荷量q=4×10-5C的带电小球从两板上方的A点以v0=4m/s的初速度水平抛出,小球恰好能从M板上端进入两板之间,并沿直线运动打到N板上的B点.已知A距两板上端的高度为h=0.2m,不计空气阻力,g=10m/s2.则( )分析:小球在进入电场前做平抛运动,根据高度求出竖直分速度的大小,结合平行四边形定则求出小球到达M板上端的速度大小以及方向.抓住小球在电场中做直线运动,合力的方向与速度的方向在同一条直线上,根据电场力的大小,结合电势差和d的关系求求出M、N板的间距,从而得出L的长度.根据动能定理求出小球到达B点的动能.
解答:解:A、小球到达M板上端时,竖直分速度vy=
=
m/s=2m/s.根据平行四边形定则知,小球到达M板上端的速度vm=
=2
m/s.故A正确.
B、速度方向与水平方向的夹角的正切值tanθ=
=
,因为小球在电场中做直线运动,知合力的方向与速度的方向在同一条直线上,有
=
,解得电场强度E=
=
=5000V/m.则M、N间距d=
=
m=0.3m.故B正确.
C、根据tanθ=
=
得,L=
d=0.15m.故C错误.
D、根据动能定理得,mg(h+L)+qU=
mvB2-
mv02,解得EkB=0.1×0.35+4×10-5×1.5×103+
×0.01×16J=0.175J.故D正确.
故选:ABD.
| 2gh |
| 2×10×0.2 |
| vy2+v02 |
| 5 |
B、速度方向与水平方向的夹角的正切值tanθ=
| vy |
| v0 |
| 1 |
| 2 |
| mg |
| qE |
| 1 |
| 2 |
| 2mg |
| q |
| 2×0.1 |
| 4×10-5 |
| U |
| E |
| 1500 |
| 5000 |
C、根据tanθ=
| L |
| d |
| 1 |
| 2 |
| 1 |
| 2 |
D、根据动能定理得,mg(h+L)+qU=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故选:ABD.
点评:解决本题的关键知道小球先做平抛运动,再做匀加速直线运动,知道在电场中所受的电场力和重力的合力与速度的方向共线.

练习册系列答案
相关题目
 如图两块平行金属板M、N竖直放置,两板间电势差U=1.5×103V.现将质量m=1×10-2kg、电荷量q=4×10-5C的带电小球从两板上方的A点以v0=4m/s的初速度水平抛出,小球恰好能从M板上端进入两板之间,并沿直线运动打到N板上的B点.已知A距两板上端的高度为h=0.2m,不计空气阻力,g=10m/s2.则( )
如图两块平行金属板M、N竖直放置,两板间电势差U=1.5×103V.现将质量m=1×10-2kg、电荷量q=4×10-5C的带电小球从两板上方的A点以v0=4m/s的初速度水平抛出,小球恰好能从M板上端进入两板之间,并沿直线运动打到N板上的B点.已知A距两板上端的高度为h=0.2m,不计空气阻力,g=10m/s2.则( )A、小球到达M板上端时的速度大小vm=2
| ||
| B、M、N两板间距d=0.3m | ||
| C、落点B距N板上端距离L=0.2m | ||
| D、小球到达B点时动能Ek=0.15J |