ЬтФПФкШн
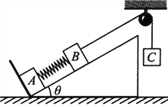
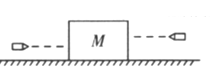
ЁОЬтФПЁП(13Зж)ШчЭМЫљЪОЃЌвЛзуЙЛГЄЕФЫЎЦНДЋЫЭДјвдЫйЖШv0дШЫйдЫЖЏЃЌжЪСПОљЮЊmЕФаЁЮяПщPКЭаЁЮяПщQгЩЭЈЙ§ЛЌТжзщЕФЧсЩўСЌНгЃЌЧсЩўзуЙЛГЄЧвВЛПЩЩьГЄЃЎФГЪБПЬЮяПщPДгДЋЫЭДјзѓЖЫвдЫйЖШ2v0ГхЩЯДЋЫЭДјЃЌPгыЖЈЛЌТжМфЕФЩўзгЫЎЦНЃЎвбжЊЮяПщPгыДЋЫЭДјМфЕФЖЏФІВСвђЪ§ІЬ=0.25ЃЌжиСІМгЫйЖШЮЊgЃЌВЛМЦЛЌТжЕФжЪСПгыФІВСЃЎЧѓЃК

ЃЈ1ЃЉдЫЖЏЙ§ГЬжааЁЮяПщPЁЂQЕФМгЫйЖШДѓаЁжЎБШЃЛ
ЃЈ2ЃЉЮяПщPИеГхЩЯДЋЫЭДјЕНгвЗНзюдЖДІЕФЙ§ГЬжаЃЌPQЯЕЭГЛњаЕФмЕФИФБфСПЃЛ
ЃЈ3ЃЉШєДЋЫЭДјвдВЛЭЌЕФЫйЖШvЃЈ0<v<2v0ЃЉдШЫйдЫЖЏЃЌЕБvШЁЖрДѓЪБЮяПщPЯђгвГхЕНзюдЖДІЪБЃЌPгыДЋЫЭДјМфВњЩњЕФФІВСШШзюаЁЃПзюаЁжЕЮЊЖрДѓЃП
ЁОД№АИЁПЃЈ1ЃЉ1:2ЃЈ2ЃЉ0ЃЈ3ЃЉ![]() ЪБЃЌФІВСШШзюаЁ
ЪБЃЌФІВСШШзюаЁ![]()
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉгЩЭМПЩжЊЃЌPгыQЕФЮЛвЦЙиЯЕЪМжеТњзуPЕФЮЛвЦЪЧQЕФЮЛвЦЕФ2БЖЃЌНсКЯЃК![]() ЧѓЕУМгЫйЖШЕФБШжЕЃЛ
ЧѓЕУМгЫйЖШЕФБШжЕЃЛ
ЃЈ2ЃЉЗжБ№вдPгыQЮЊбаОПЕФЖдЯѓЃЌгЩХЃЖйЕкЖўЖЈТЩЧѓГіМгЫйЖШЃЌШЛКѓНсКЯдЫЖЏбЇЕФЙЋЪНЃЌЧѓГіPгыДЋЫЭДјЕФЫйЖШЯрЕШжЎЧАЕФЮЛвЦЃЛЕБPЕФЫйЖШгыДЋЫЭДјЯрЕШКѓЃЌЗжЮіФІВССІгыЩўзгЕФРСІЕФЙиЯЕЃЌХаЖЯГіPНЋМЬајМѕЫйЃЌЧѓГіМгЫйЖШЃЌдкНсКЯдЫЖЏбЇЕФЙЋЪНЧѓГіЮЛвЦЃЌзюКѓгЩЙІФмЙиЯЕЧѓГіЛњаЕФмЕФИУБфСПЃЛ
ЃЈ3ЃЉНсКЯЃЈ2ЃЉЕФНтД№Й§ГЬЃЌаДГіЮяЬхPЯрЖдгкДЋЫЭДјЕФЮЛвЦЕФБэДяЪНвдМАQ=fxЯрЖдЃЌШЛКѓМДПЩЧѓГіВњЩњЕФзюаЁЕФШШСПЃЎ
НтЃКЃЈ1ЃЉЩшPЕФЮЛвЦЁЂМгЫйЖШДѓаЁЗжБ№ЮЊs1ЁЂa1ЃЌQЕФЮЛвЦЁЂМгЫйЖШДѓаЁЗжБ№ЮЊs2ЁЂa2ЃЌ
вђs1="2" s2ЃЌЙЪa1=2a2![]()
ЃЈ2ЃЉЖдPгаЃКІЬmg+T=ma1
ЖдQгаЃКmgЉ2T=ma2
ЕУЃКT=0.35mgЃЌa1=0.6g
PЯШМѕЫйЕНгыДЋЫЭДјЫйЖШЯрЭЌЃЌЩшЮЛвЦЮЊx1ЃЌ
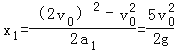
ЙВЫйКѓЃЌгЩгкf=ІЬmgЃМ![]() mgЃЌPВЛПЩФмЫцДЋЫЭДјвЛЦ№дШЫйдЫЖЏЃЌМЬајЯђгвМѕЫйЃЌ
mgЃЌPВЛПЩФмЫцДЋЫЭДјвЛЦ№дШЫйдЫЖЏЃЌМЬајЯђгвМѕЫйЃЌ
ЩшДЫЪБPМгЫйЖШЮЊa1ЁфЃЌQЕФМгЫйЖШЮЊ![]()
ЖдPгаЃКTЉІЬmg=ma1ЁфЃЌЖдQгаЃКmgЉ2T=ma2ЁЏНтЕУЃКa1Ёф=0.2g
ЩшМѕЫйЕН0ЮЛвЦЮЊx2ЃЌ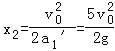
PQЯЕЭГЛњаЕФмЕФИФБфСПЕШгкФІВССІЖдPзіЕФЙІЃЌЁїE=ЉІЬmgx1+ІЬmgx2=0
ЃЈ3ЃЉЕквЛНзЖЮPЯрЖдЦЄДјЯђЧАЃЌЯрЖдТЗГЬЃК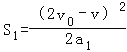
ЕкЖўНзЖЮЯрЖдЦЄДјЯђКѓЃЌЯрЖдТЗГЬЃК![]()
ФІВСВњЩњЕФШШQ=ІЬmgЃЈS1+S2ЃЉ=![]()
ЕБ![]() ЪБЃЌ
ЪБЃЌ
ФІВСШШзюаЁ![]()
Д№ЃКЃЈ1ЃЉдЫЖЏЙ§ГЬжааЁЮяПщPЁЂQЕФМгЫйЖШДѓаЁжЎБШЪЧ2ЃК1ЃЛ
ЃЈ2ЃЉЮяПщPИеГхЩЯДЋЫЭДјЕНгвЗНзюдЖДІЕФЙ§ГЬжаЃЌPQЯЕЭГЛњаЕФмЕФИФБфСПЃЛ
ЃЈ3ЃЉШєДЋЫЭДјвдВЛЭЌЕФЫйЖШvЃЈ0ЃМvЃМ2v0ЃЉдШЫйдЫЖЏЃЌЕБ![]() ЪБЮяПщPЯђгвГхЕНзюдЖДІЪБЃЌPгыДЋЫЭДјМфВњЩњЕФФІВСШШзюаЁЃЌзюаЁжЕЮЊ
ЪБЮяПщPЯђгвГхЕНзюдЖДІЪБЃЌPгыДЋЫЭДјМфВњЩњЕФФІВСШШзюаЁЃЌзюаЁжЕЮЊ![]()