题目内容
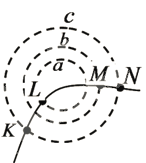
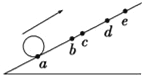
【题目】如图所示，小球沿足够长的斜面向上做匀变速直线运动，依次经a、b、c、d到达最高点e．已知ab=bd=6m，bc=1m，小球从a到c和从c到d所用的时间都是2s，设小球经b、c时的速度分别为vb、vc，则：
（1）vb、vc分别为多少？
（2）Xde=？
（3）从d到e所用时间为多少？
【答案】(1）vb、vc分别为3m/s， 
m/s ；（2）Xde=4m；
（3）从d到e所用时间为4s．
【解析】试题分析：从a到c和从c到d所用时间都是2s，运用匀变速直线运动的中间时刻的瞬时速度等于全程的平均速度可以直接求出C点的速，根据△x=aT2可以求出小球的加速度a，在从b到c的过程中已知小球的加速度a和位移及c点的速度，根据匀变速直线运动的速度位移关系可以求出小球在b的速度，已知c点的速度，和加速度可以求出ce的距离以及从c到e所用的时间．
（1）因为c是从a到d的时间中点，根据
知，小球在c点的瞬时速度为：
=
=
根据匀变速直线运动的规律的推论有：△x=aT2，知小球运动的加速度：
a=
=
=
=
根据匀变速直线运动的速度位移关系有：
得：
=
=
（2）从c至e小球做匀减速直线运动，根据速度位移关系有：
得：
=
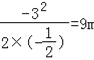，因为cd=5m，所以de=4m；
（3）从c到e所用时间为：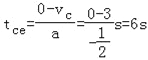
.
练习册系列答案
相关题目
