题目内容
【题目】现有一根长L=1m的刚性轻绳,其一端固定于O点,另一端系着质量m=0.5kg的小球(可视为质点),将小球提至O点正上方的A点处,此时绳刚好伸直且无张力,如图所示。不计空气阻力,取g=10m/s2,则:
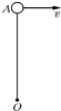
(1)在小球以速度v1=4m/s水平抛出的瞬间,绳中的张力为多少?
(2)在小球以速度v2=1m/s水平抛出的瞬间,绳中若有张力,求其大小;若无张力,试求绳子再次伸直时所经历的时间。
(3)接上问,当小球摆到最低点时,绳子拉力的大小是多少?
【答案】(1)3N(2)0.6s(3)10.92N或者![]()
【解析】试题分析:根据判断可以知道![]() ,故绳中有张力,由向心力的公式可以求得绳的拉力的大小;由于
,故绳中有张力,由向心力的公式可以求得绳的拉力的大小;由于![]() ,故绳中没有张力,小球将做平抛运动,根据平抛运动的规律可以求得运动的时间.
,故绳中没有张力,小球将做平抛运动,根据平抛运动的规律可以求得运动的时间.
(1)绳子刚好无拉力时对应的临界速度满足![]() ,解得
,解得![]()
因为![]() ,所以绳子有拉力且满足
,所以绳子有拉力且满足![]() ,解得
,解得![]()
(2)因为![]() ,所以绳子无拉力,小球以
,所以绳子无拉力,小球以![]() 作平抛运动
作平抛运动
设经过t后绳子再次伸直,则满足方程![]()
其中![]() ,
, ![]() ,解得t=0.6s
,解得t=0.6s
(3)当t=0.6s时,可得x=0.6m,y=1.8m,小球在O点右下方位置,且O与小球连线与竖直方向的夹角满足![]()
且此时速度的水平分量与竖直分量分别为![]() ,
, ![]()
绳伸直的一瞬间,小球的速度沿绳分量突变为零,只剩下垂直于绳子方向的速度![]()
接着小球以![]() 为初速度绕着O作圆周运动摆到最低点,设最低点速度为v
为初速度绕着O作圆周运动摆到最低点,设最低点速度为v
则![]() ,
, ![]() ,解得
,解得![]() 或10.92N
或10.92N

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目