题目内容
【题目】质量为m=0.5 kg、长L=1 m的平板车B静止在光滑水平面上,某时刻质量M=l kg的物体A(视为质点)以v0=4 m/s向右的初速度滑上平板车B的上表面,在A滑上B的同时,给B施加一个水平向右的拉力。已知A与B之间的动摩擦因数μ=0.2,重力加速度g取10 m/s2。试求:
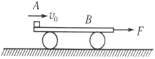
(1)如果要使A不至于从B上滑落,拉力F大小应满足的条件;
(2)若F=5 N,物体A在平板车上运动时相对平板车滑行的最大距离。
【答案】(1)![]() (2)
(2)![]()
【解析】
物体A不滑落的临界条件是A到达B的右端时,A、B具有共同的速度,结合牛顿第二定律和运动学公式求出拉力的最小值.另一种临界情况是A、B速度相同后,一起做匀加速直线运动,根据牛顿第二定律求出拉力的最大值,从而得出拉力F的大小范围.
(1)物体A不滑落的临界条件是A到达B的右端时,A、B具有共同的速度v1,则:![]()
又: ![]()
解得:aB=6m/s2
再代入F+μMg=maB得:F=1N
若F<1N,则A滑到B的右端时,速度仍大于B的速度,于是将从B上滑落,所以F必须大于等于1N
当F较大时,在A到达B的右端之前,就与B具有相同的速度,之后,A必须相对B静止,才不会从B的左端滑落,则由牛顿第二定律得:
对整体:F=(m+M)a
对物体A:μMg=Ma
解得:F=3N
若F大于3N,A就会相对B向左滑下
综上所述,力F应满足的条件是1N≤F≤3N
(2)物体A滑上平板车B以后,做匀减速运动,由牛顿第二定律得:μMg=MaA
解得:aA=μg=2m/s2
平板车B做匀加速直线运动,由牛顿第二定律得:F+μMg=maB
解得:aB=14m/s2
两者速度相同时物体相对小车滑行最远,有:v0-aAt=aBt
解得:t=0.25s
A滑行距离 xA=v0t-![]() aAt2=
aAt2=![]() m
m
B滑行距离:xB=![]() aBt2=
aBt2=![]() m
m
最大距离:Δx=xA-xB=0.5m

【题目】图甲为某同学用力传感器去探究弹簧的弹力和伸长量的关系的实验情景。用力传感器竖直向下拉上端固定于铁架台的轻质弹簧,读出不同拉力下的标尺刻度x及拉力大小F(从电脑中直接读出)。所得数据记录在下列表格中:
拉力大小F/N | 0.45 | 0.69 | 0.93 | 1.14 | 1.44 | 1.69 |
标尺刻度x/cm | 57.02 | 58.01 | 59.00 | 60.00 | 61.03 | 62.00 |
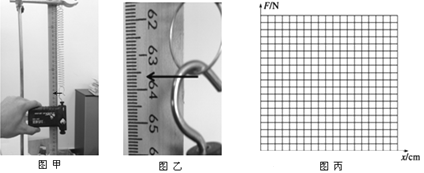
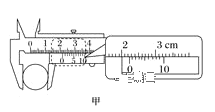
(1)从图乙读出刻度尺上的刻度值为 cm;
(2)根据所测数据,在图丙坐标纸上作出F与x的关系图象;
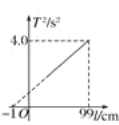
(3)由图象求出该弹簧的劲度系数为 N/m、弹簧的原长为 cm。(均保留三位有效数字)