题目内容
倾角θ=37°的斜面体固定在水平地面上，一根轻绳跨过固定在斜面顶端的定滑轮，绳的一端与质量为ml=1kg的物块A连接，且绳与斜面平行；另一端与质量为m2=3kg的物块B连接．开始时，用手按住A，使B悬于距地面高H=0.6m处，而A静止于斜面底端．如图所示．现释放B，试求此后A在斜面上向上滑行的最大距离？（设斜面足够长，且所有接触面间的摩擦均忽略不计，sin37°=0.6，cos37°=0.8，g取10m/s2）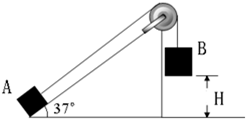
设B落地时的速度为v，系统的机械能守恒：
m2gH-m1gHsinθ=
（m1+m2）v2 ①
B落地后，A以v为初速度沿斜面匀减速上升，设沿斜面又上升的距离为S，
由动能定理得：-m1gSsinθ=0-
mv2 ②
物体m能沿斜面滑行的最大距离：L=h+S ③
由①②③代入数据得：L=1.2m
答：物体A能沿斜面滑行的最大距离是1.2m．
m2gH-m1gHsinθ=
| 1 |
| 2 |
B落地后，A以v为初速度沿斜面匀减速上升，设沿斜面又上升的距离为S，
由动能定理得：-m1gSsinθ=0-
| 1 |
| 2 |
物体m能沿斜面滑行的最大距离：L=h+S ③
由①②③代入数据得：L=1.2m
答：物体A能沿斜面滑行的最大距离是1.2m．
练习册系列答案
相关题目
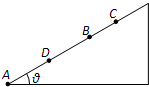某物体以初动能E0从倾角θ=37°的斜面底部A点沿斜面上滑，物体与斜面间的动摩擦因数μ=0.5．当物体滑到B点时动能为E，滑到C点时动能为0，物体从C点下滑到AB中点D时动能又为E，则下列说法正确的是（已知|AB|=s，sin37°=0.6，cos37°=0.8）（ ）
如图所示，在水平地面上固定一倾角θ=37°的斜面体，物体A以某一初速度从斜面体底端沿斜面向上抛出，在物体A的正上方，有一物体B以某一初速度水平抛出．A、B均可看作质点，已知sin37°=0.6，cos37°=0.8，g取10m/s2．
物体A在水平力F1=500N的作用下，沿倾角θ=37°的斜面匀速上滑，物休A所受的重力G=500N．求斜面对物体A的支持力和A与斜面的动摩擦因数μ．（sin37°=0.6，cos37°=0.8）
质量为40kg的雪橇在倾角θ=37°的斜面上向下滑动如图甲所示，所受的空气阻力与速度成正比．今测得雪橇运动的v-t图象如图乙所示，且AB是曲线的切线，B点坐标为（4，15），CD是曲线的渐近线，g取10m/s2．根据以上信息，不可以确定下列哪个物理量（ ）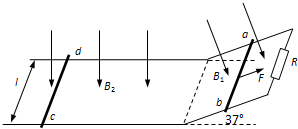
如图所示，两条间距l=1m的光滑金属导轨制成倾角37°的斜面和水平面，上端用阻值为R=4Ω的电阻连接．在斜面导轨区域和水平导轨区域内分别有垂直于斜面和水平面的匀强磁场B1 和B2，且B1=B2=0.5T．ab和cd是质量均为m=0.1kg，电阻均为r=4Ω的两根金属棒，ab置于斜面导轨上，cd置于水平导轨上，均与导轨垂直且接触良好．已知t=0时刻起，cd棒在外力作用下开始水平向右运动（cd棒始终在水平导轨上运动），ab棒受到F=0.6-0.2t（N）沿斜面向上的力作用，处于静止状态．不计导轨的电阻，试求：