题目内容
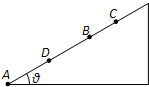 某物体以初动能E0从倾角θ=37°的斜面底部A点沿斜面上滑,物体与斜面间的动摩擦因数μ=0.5.当物体滑到B点时动能为E,滑到C点时动能为0,物体从C点下滑到AB中点D时动能又为E,则下列说法正确的是(已知|AB|=s,sin37°=0.6,cos37°=0.8)( )
某物体以初动能E0从倾角θ=37°的斜面底部A点沿斜面上滑,物体与斜面间的动摩擦因数μ=0.5.当物体滑到B点时动能为E,滑到C点时动能为0,物体从C点下滑到AB中点D时动能又为E,则下列说法正确的是(已知|AB|=s,sin37°=0.6,cos37°=0.8)( )分析:分别对AB及从A返回D的过程由动能定理列式,联立可求得BC的长度;对全程列式可求得回到A点的动能.
解答:解:对AB有:-mgssinθ-μmgscosθ=E-E0;
设BC为L,对从A到最高点再返回到D过程有:
-mg
sinθ-μmg(s+
+2L)cosθ=E-E0;
联立解得:
mg
sinθ=μmg(
+2L)cosθ
代入数据得:L=
,故A错误,B正确;
对A到C有:
-mg(s+L)sinθ-μm(s+L)gcosθ=0-E0;
解得:
E0=mg(s+L)sinθ+μmg(s+L)cosθ=mg(s+L)(sinθ+μcosθ)=
mgs
即:mgs=
E0;
对全程有:-μmg(2s+2L)cosθ=E′-E0;
E′=0.9mgs-E0=-0.8E0+E0=
故D正确;
故选BD.
设BC为L,对从A到最高点再返回到D过程有:
-mg
| s |
| 2 |
| s |
| 2 |
联立解得:
mg
| s |
| 2 |
| s |
| 2 |
代入数据得:L=
| s |
| 8 |
对A到C有:
-mg(s+L)sinθ-μm(s+L)gcosθ=0-E0;
解得:
E0=mg(s+L)sinθ+μmg(s+L)cosθ=mg(s+L)(sinθ+μcosθ)=
| 9 |
| 8 |
即:mgs=
| 8 |
| 9 |
对全程有:-μmg(2s+2L)cosθ=E′-E0;
E′=0.9mgs-E0=-0.8E0+E0=
| E0 |
| 5 |
故D正确;
故选BD.
点评:本题过程较多需要的物理是也多,但题目中给出的物理是量确较少,故应引入中间量,在解题时要注意是后的结果的转化.本题也可先求出上滑的加速度和下滑的加速度,结合牛顿运动定律和能量进行求解.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
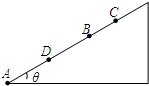 某物体以初动能E0从倾角θ=37°的斜面底部A点沿斜面上滑,物体与斜面间的动摩擦因数μ=0.5.当物体滑到B点时动能为E,滑到C点时动能为0,物体从C点下滑到AB中点D时动能又为E,则下列说法正确的是(已知|AB|=s,sin37°=0.6,cos37°=0.8)( )
某物体以初动能E0从倾角θ=37°的斜面底部A点沿斜面上滑,物体与斜面间的动摩擦因数μ=0.5.当物体滑到B点时动能为E,滑到C点时动能为0,物体从C点下滑到AB中点D时动能又为E,则下列说法正确的是(已知|AB|=s,sin37°=0.6,cos37°=0.8)( )A、BC段的长度为
| ||
B、BC段的长度为
| ||
C、物体再次返回A点时的动能为
| ||
D、物体再次返回A点时的动能为
|

 A.BC段的长度为
A.BC段的长度为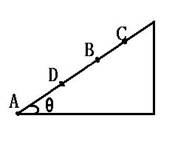 某物体以初动能E0从倾角θ=37°的斜面底A点沿斜面上滑,物体与斜面间的摩擦系数μ=0.5,而且mgsinθ>μmgcosθ。当物体滑到B点时动能为E,滑到C点时动能为0,物体从C点下滑到AB中点D时动能又为E。已知AB=s,求BC的长度。
某物体以初动能E0从倾角θ=37°的斜面底A点沿斜面上滑,物体与斜面间的摩擦系数μ=0.5,而且mgsinθ>μmgcosθ。当物体滑到B点时动能为E,滑到C点时动能为0,物体从C点下滑到AB中点D时动能又为E。已知AB=s,求BC的长度。