物体A在水平力F1=500N的作用下.沿倾角θ=37°的斜面匀速上滑.物休A所受的重力G=500N．求斜面对物体A的支持力和A与斜面的动摩擦因数μ．(sin37°=0.6.cos37°=0.8) 题目和参考答案——青夏教育精英家教网—

题目内容

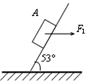
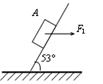
物体A在水平力F₁=500N的作用下，沿倾角θ=37°的斜面匀速上滑，物休A所受的重力G=500N．求斜面对物体A的支持力和A与斜面的动摩擦因数μ．（sin37°=0.6，cos37°=0.8）

分析：对物体受力分析，抓住沿斜面方向和垂直于斜面方向合力为零，求出支持力和摩擦力的大小，结合滑动摩擦力的大小公式求出动摩擦因数的大小．

解答：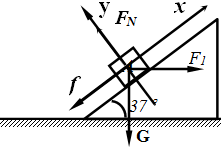

解：取A为研究对象，受力如图，并建立如图坐标．
由平衡条件可知，在坐标X、Y两个方向合力分为零，即有
X轴：F₁cos37°-Gsin37°-f=0①
Y轴：F_N-F₁sin37°-Gcos37°=0②
由②式解得F_N=700N
由②式解得f=100N
所以μ=

100

700

=0.14
答：斜面对物体A的支持力为700N，A与斜面的动摩擦因数μ为0.14．

点评：解决本题的关键能够正确地受力分析，运用共点力平衡进行求解．

练习册系列答案

1加1阅读好卷系列答案

相关题目

物体A在水平力F₁＝500 N的作用下，沿倾角θ＝37°的斜面匀速上滑，物休A所受的重力G＝500 N．求斜面对物体A的支持力和A与斜面的动摩擦因数μ．

(sin37°＝0.6，cos37°＝0.8)

物体A在水平力F₁=500N的作用下，沿倾角θ=的斜面匀速上滑，物休A所受的重力G=500N。求斜面对物体A的支持力和A与斜面的动摩擦因数μ。

（sin=0.6，cos=0.8）

物体A在水平力F₁=400N的作用下，沿倾角θ=53°的斜面匀速下滑，如图所示。物体A受的重力G=400N，求斜面对物体A的支持力和A与斜面间的动摩擦因数μ。（sin53°=0.8，cos53°=0.6）

试题分类