题目内容
8.真空中有两个相同的带电金属小球A和B,相距为r,带电量分别为q和2q,它们之间相互作用力的大小为F.有一个不带电的金属球C,大小跟A、B相同,当C跟A、B小球各接触一次后拿开,再将A、B间距离变为2r,那么A、B间的作用力的大小可为( )| A. | $\frac{3F}{64}$ | B. | 0 | C. | $\frac{3F}{32}$ | D. | $\frac{3F}{16}$ |
分析 完全相同的带电金属球相碰时,总电量平分.分两种情况:第一情况,C先与A接触再与B接触;第二情况,C先与B接触再与A接触,分别求出A、B两球的带电量,再由库仑定律研究后来A、B间的作用力的大小可能值.
解答 解:(1)若AB两球带同种电荷,则有:
若C先与A接触再与B接触,A的带电量为$\frac{q}{2}$,B的带电量为$\frac{\frac{q}{2}+2q}{2}$=$\frac{5}{4}q$
根据库仑定律得:
C与A、B接触前:F=2$\frac{k{q}^{2}}{{r}^{2}}$
C与A、B接触后:F1═$\frac{k\frac{q}{2}•\frac{5q}{4}}{(2r)^{2}}$=$\frac{5}{32}\frac{k{q}^{2}}{{r}^{2}}$;
则有F1=$\frac{5}{64}F$
若C先与B接触再与A接触,B的带电量为q,A的带电量为q,则库仑力变为$\frac{F}{4}$.
(2)若AB两球带异种电荷,则有:
若C先与A接触再与B接触,A的带电量为-$\frac{q}{2}$,B的带电量为$\frac{-\frac{q}{2}+2q}{2}$=$\frac{3q}{4}$
根据库仑定律得:
C与A、B接触前:F=2$\frac{k{q}^{2}}{{r}^{2}}$
C与A、B接触后:F1=$\frac{3F}{64}$F
若C先与B接触再与A接触,B的带电量为q,A的带电量为0,则库仑力变为0,
由以上情况可知,BC正确,AD错误;
故选:BC.
点评 本题是库仑定律的应用问题,关键确定小球接触后的电量,要注意明确所有的可能性,注意C球先和哪个球接触的结果也不相同.

练习册系列答案
相关题目
17.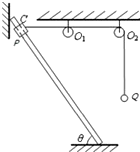 如图所示,一轻绳绕过无摩擦的两个轻质小定滑轮O1、O2分别与质量均为m的小滑块P和小球Q连接.已知光滑直杆两端固定且与两定滑轮在同一竖直平面内,杆与水平面的夹角为θ,直杆上C点与两定滑轮均在同一高度.设直杆足够长,小球运动过程中不会与其他物体相碰.现将小物块从C点由静止释放,在其下滑过程中,下列说法正确的是( )
如图所示,一轻绳绕过无摩擦的两个轻质小定滑轮O1、O2分别与质量均为m的小滑块P和小球Q连接.已知光滑直杆两端固定且与两定滑轮在同一竖直平面内,杆与水平面的夹角为θ,直杆上C点与两定滑轮均在同一高度.设直杆足够长,小球运动过程中不会与其他物体相碰.现将小物块从C点由静止释放,在其下滑过程中,下列说法正确的是( )
 如图所示,一轻绳绕过无摩擦的两个轻质小定滑轮O1、O2分别与质量均为m的小滑块P和小球Q连接.已知光滑直杆两端固定且与两定滑轮在同一竖直平面内,杆与水平面的夹角为θ,直杆上C点与两定滑轮均在同一高度.设直杆足够长,小球运动过程中不会与其他物体相碰.现将小物块从C点由静止释放,在其下滑过程中,下列说法正确的是( )
如图所示,一轻绳绕过无摩擦的两个轻质小定滑轮O1、O2分别与质量均为m的小滑块P和小球Q连接.已知光滑直杆两端固定且与两定滑轮在同一竖直平面内,杆与水平面的夹角为θ,直杆上C点与两定滑轮均在同一高度.设直杆足够长,小球运动过程中不会与其他物体相碰.现将小物块从C点由静止释放,在其下滑过程中,下列说法正确的是( )| A. | 小滑块P的动能先增加后减小 | B. | 小滑块P的机械能先减小后增加 | ||
| C. | 小球Q的动能先增加后减小 | D. | 小球Q的机械能先减小后增加 |
16. 如图所示,一足够长的木板静止在光滑水平面上,一物块静止在木板上,木板和物块间有摩擦.现用水平恒力向右拉木板,当物块相对木板滑动了一段距离但仍有相对运动时,撤掉拉力,此后木板和物块相对于水平面的运动情况为( )
如图所示,一足够长的木板静止在光滑水平面上,一物块静止在木板上,木板和物块间有摩擦.现用水平恒力向右拉木板,当物块相对木板滑动了一段距离但仍有相对运动时,撤掉拉力,此后木板和物块相对于水平面的运动情况为( )
 如图所示,一足够长的木板静止在光滑水平面上,一物块静止在木板上,木板和物块间有摩擦.现用水平恒力向右拉木板,当物块相对木板滑动了一段距离但仍有相对运动时,撤掉拉力,此后木板和物块相对于水平面的运动情况为( )
如图所示,一足够长的木板静止在光滑水平面上,一物块静止在木板上,木板和物块间有摩擦.现用水平恒力向右拉木板,当物块相对木板滑动了一段距离但仍有相对运动时,撤掉拉力,此后木板和物块相对于水平面的运动情况为( )| A. | 物块先向左运动,再向右运动 | |
| B. | 木板向右运动,速度逐渐减小,直到为零 | |
| C. | 物块向右运动,速度逐渐增大,直到做匀速运动 | |
| D. | 木板和物块的速度都逐渐变小,直到为零 |
3.一质点做直线运动,在第1s、第2s、第3s、第4s末的速度分别为v1=1m/s,v2=2m/s,v3=4m/s,v4=8m/s,则这个质点的运动 是( )
| A. | 匀速直线运动 | B. | 匀加速直线运动 | ||
| C. | 匀减速直线运动 | D. | 非匀变速直线运动 |
20.如果取弹簧伸长△x时的弹性势能为0,则下列说法中正确的是( )
| A. | 弹簧处于原长时,弹簧弹性势能为正值 | |
| B. | 弹簧处于原长时,弹簧弹性势能为0 | |
| C. | 当弹簧的压缩量为△x时,弹性势能的值为0 | |
| D. | 只要弹簧被压缩,弹性势能就为负值 |
18.一个物体从静止出发以加速度a做匀加速直线运动,经过时间t后,紧接着以该时刻的速度做匀速直线运动,运动时间也为t,则在2t时间内的平均速度是( )
| A. | 0.5at | B. | 0.75at | C. | 3at | D. | 1.25at |
 当前“雾霾”成为全社会关注的热点,为了缓解空气污染,我国多地市启动了“光伏工程”示范项目,在屋顶安装太阳能光伏板,如图所示是某中学的教学楼顶安装了总功率为20kW的光伏发电系统.按一天的有效光照时间8h计算,该中学光伏发电系统一天共发电160kw•h,这些发电量如果由热电转换效率为30%的热电厂来完成,需要燃烧64kg煤;你一定很关注“雾霾天气”的报道,请结合所了解的知识,谈谈家庭光伏发电的优点:减少污染、节约能源(谈一点即可).(煤的热值q煤=3.0×107J/kg )
当前“雾霾”成为全社会关注的热点,为了缓解空气污染,我国多地市启动了“光伏工程”示范项目,在屋顶安装太阳能光伏板,如图所示是某中学的教学楼顶安装了总功率为20kW的光伏发电系统.按一天的有效光照时间8h计算,该中学光伏发电系统一天共发电160kw•h,这些发电量如果由热电转换效率为30%的热电厂来完成,需要燃烧64kg煤;你一定很关注“雾霾天气”的报道,请结合所了解的知识,谈谈家庭光伏发电的优点:减少污染、节约能源(谈一点即可).(煤的热值q煤=3.0×107J/kg )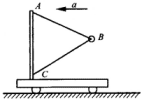 如图所示,AB=BC=AC=1m,小球的质量为1kg,当小车的加速度大于$\sqrt{3}g$时,BC绳开始有拉力;当两绳均有拉力时,两绳拉力之差为2mgN.
如图所示,AB=BC=AC=1m,小球的质量为1kg,当小车的加速度大于$\sqrt{3}g$时,BC绳开始有拉力;当两绳均有拉力时,两绳拉力之差为2mgN.