Question

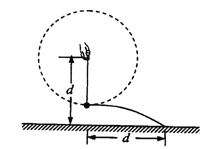
【题目】如图所示，小明站在水平地面上，手握不可伸长的轻绳一端，绳的另一端系有质量为m的小球，甩动手腕，使球在竖直平面内做圆周运动。当球某次运动到最低点时，绳突然断掉，球飞行水平距离d后落地。已知握绳的手离地面高度为d，手与球之间的绳长为，重力加速度为g。忽略手的运动半径和空气阻力。

（1）若想小球在竖直平面内做完整的圆周运动，其通过最高点的速度至少应为多少？

（2）求绳断时球的速度大小和球落地时的速度大小。

（3）轻绳能承受的最大拉力多大？

Answer 1

【答案】(1) (2) ， （3）

【解析】试题分析：若想小球在竖直平面内做完整的圆周运动，其在最高点时重力提供向心力即可求出速度；根据平抛运动的高度求出平抛运动的时间，结合水平位移和时间求出绳断时球的速度，根据动能定理求出球落地的速度大小；在最低点，根据牛顿第二定律求出最大拉力的大小。

（1）若想小球在竖直平面内做完整的圆周运动，其在最高点时，满足，

解得：；

（2）设绳断后球飞行时间为t，由平抛运动规律，知，在水平和竖直两方向上分别有：

竖直：，水平：，

解得：，

落地时其竖直分速度为：，

落地时速度为：；

（3）设绳子承受的最大拉力为，这也是球受到绳的最大拉力

球做圆周运动的半径为：，

在最低点时球受到的合力提供向心力，即：

解得：