题目内容
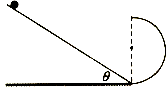
【题目】如图所示,倾角为θ的光滑倾斜轨道在最底端与一半径为r的光滑半圆弧轨通过极短的一小段光滑曲轨道平滑连接,使半圆轨道的最高点、圆心、最低点在同一竖直线上,让一小球从倾斜轨道上某一位置由静止释放,沿倾斜轨道和半圆弧轨道运动,经过圆弧的顶点水平抛出,试判断小球有没有可能垂直落在斜面上,若能,斜面倾角应满足什么条件?若不能,请说明理由。
【答案】小球能垂直落在斜面上,斜面倾角应满足![]()
【解析】
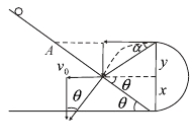
试题分析: 设小球从圆弧顶点以速度v0抛出,经过时间t秒垂直落在斜面上,斜面的倾角为θ.如图所示:
则要使小球能通过最高点,需满足:![]()
解得:![]()
到达斜面时,满足:![]()
得:![]()
竖直方向位移:![]() ,解得:
,解得:![]()
落点到最低点的高度差为x,且![]() ,解得
,解得![]()
由几何院系知![]()
联立得:![]()
若能垂直落在斜面上要满足:![]()
上式有解,且解得![]()
即小球能垂直落在斜面上,斜面倾角应满足![]()

练习册系列答案
相关题目
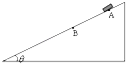
【题目】如图所示,斜面倾角为θ,斜面上AB段光滑,其它部分粗糙,且斜面足够长.一带有速度传感器的小物块(可视为质点),自A点由静止开始沿斜面下滑,速度传感器上显示的速度与运动时间的关系如下表所示:
时间(s) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | …. |
速度(m/s) | 0 | 6 | 12 | 17 | 21 | 25 | 29 | … |
取g=10m/s2,求:
(1)斜面的倾角θ多大?
(2)小物块与斜面的粗糙部分间的动摩擦因数μ为多少?
(3)AB间的距离xAB等于多少?