题目内容
18. 如图所示,两根轻弹簧AC和BD,它们的劲度系数分别为k1和k2,它们的C、D端分别固定在质量为m的物体上,A、B端分别固定在支架和正下方地面上,当物体m静止时,上方的弹簧处于原长;若将物体的质量变为3m,仍在弹簧的弹性限度内,当物体再次静止时,其相对第一次静止时位置下降了( )
如图所示,两根轻弹簧AC和BD,它们的劲度系数分别为k1和k2,它们的C、D端分别固定在质量为m的物体上,A、B端分别固定在支架和正下方地面上,当物体m静止时,上方的弹簧处于原长;若将物体的质量变为3m,仍在弹簧的弹性限度内,当物体再次静止时,其相对第一次静止时位置下降了( )| A. | mg$\frac{{k}_{1}+{k}_{2}}{{k}_{1}{k}_{2}}$ | B. | 2mg$\frac{{k}_{1}+{k}_{2}}{{k}_{1}{k}_{2}}$ | ||
| C. | 2mg$\frac{1}{{k}_{1}+{k}_{2}}$ | D. | mg$\frac{1}{{k}_{1}+{k}_{2}}$ |
分析 当物体的质量为m时,下方弹簧的弹力等于mg,由胡克定律求出其压缩的长度.将物体的质量增为原来的3倍时,上方的弹簧伸长的长度与下方弹簧压缩量增加的长度相等,等于物体下降的高度,两弹簧弹力之和等于3mg,再由胡克定律求解物体下降的高度.
解答 解:当物体的质量为m时,下方弹簧压缩的长度为x2=$\frac{mg}{{k}_{2}}$.①
当物体的质量变为3m时,设物体下降的高度为x,则上方弹簧伸长的长度为x,下方弹簧被压缩的长度为x2+x,两弹簧弹力之和等于3mg由胡克定律和平衡条件得:
k1x+k2(x2+x)=3mg ②
由①②联立解得,x=2mg$\frac{1}{{k}_{1}+{k}_{2}}$
故选:C
点评 本题由胡克定律和平衡条件分别研究两种情况下弹簧的压缩量,要抓住第二情况下,两弹簧形变量与物体下降高度相等进行列式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8. 如图所示,在匀速转动的圆筒内壁上有一物体随圆筒一起转动而未滑动.若圆筒和物体以更大的角速度做匀速转动,则下列说法正确的是( )
如图所示,在匀速转动的圆筒内壁上有一物体随圆筒一起转动而未滑动.若圆筒和物体以更大的角速度做匀速转动,则下列说法正确的是( )
 如图所示,在匀速转动的圆筒内壁上有一物体随圆筒一起转动而未滑动.若圆筒和物体以更大的角速度做匀速转动,则下列说法正确的是( )
如图所示,在匀速转动的圆筒内壁上有一物体随圆筒一起转动而未滑动.若圆筒和物体以更大的角速度做匀速转动,则下列说法正确的是( )| A. | 物体所受弹力增大,摩擦力也增大 | B. | 物体所受弹力增大,摩擦力减小 | ||
| C. | 物体所受弹力增大,摩擦力不变 | D. | 物体所受弹力减小,摩擦力也减小 |
9.“嫦娥二号”绕月卫星于2010年10月1日18时59分57秒在西昌卫星发射中心发射升空,并获得了圆满成功.“嫦娥二号”新开辟了地月之间的“直航航线”,即直接发射至地月转移轨道,再进入距月面约h=l×l05m的圆形工作轨道,开始进行科学探测活动.设月球半径为R,月球表面的重力加速度为g月,万有引力常量为G,则下列说法正确的是( )
| A. | 由题目条件可知月球的平均密度为$\frac{3{g}_{月}}{4πGR}$ | |
| B. | “嫦娥二号”在工作轨道上绕月球运行的周期为2π$\sqrt{\frac{R}{{g}_{月}}}$ | |
| C. | “嫦娥二号”在工作轨道上的绕行速度为$\sqrt{{g}_{月}(R+h)}$ | |
| D. | “嫦娥二号”在工作轨道上运行时的向心加速度为($\frac{R}{R+h}$)2g月 |
6.如图甲所示,M是一个小型理想变压器,原副线圈匝数之比n1:n2=10:1,接线柱a、b接上一个正弦交变电源,电压随时间变化规律如图乙所示.变压器右侧部分为一火警报警系统原理图,其中R2为用半导体热敏材料(电阻随温度升高而减小)制成的传感器,R1为一定值电阻.下列说法中正确的是( )

| A. | 电压表V示数为22V | |
| B. | 此交变电源的频率为50Hz | |
| C. | 当传感器R2所在处出现火警时,A的示数减小 | |
| D. | 当传感器R2所在处出现火警时,V的示数减小 |
13.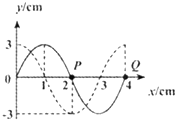 一横波在某时刻f的波形如图中实线所示.经过时间0.6s后波形曲线如图中虚线所示,已知波的周期大于0.6s.在这段时间内质点P通过的路程为0.09cm,则该波的波速为( )
一横波在某时刻f的波形如图中实线所示.经过时间0.6s后波形曲线如图中虚线所示,已知波的周期大于0.6s.在这段时间内质点P通过的路程为0.09cm,则该波的波速为( )
 一横波在某时刻f的波形如图中实线所示.经过时间0.6s后波形曲线如图中虚线所示,已知波的周期大于0.6s.在这段时间内质点P通过的路程为0.09cm,则该波的波速为( )
一横波在某时刻f的波形如图中实线所示.经过时间0.6s后波形曲线如图中虚线所示,已知波的周期大于0.6s.在这段时间内质点P通过的路程为0.09cm,则该波的波速为( )| A. | 0.05m/s | B. | 0.10m/s | C. | 0.20m/s | D. | 0.30m/s |
10.关于天然放射现象,下列叙述正确的是( )
| A. | 在α、β、γ这三种射线中,γ射线的穿透能力最强 | |
| B. | β衰变所释放的电子是原子核外的电子电离形成的 | |
| C. | 放射性元素的原子核内的核子有半数发生变化所需的时间就是半衰期 | |
| D. | 铀核(${\;}_{2}^{238}$U)衰变为铅核(${\;}_{82}^{206}$Pb)的过程中,要经过8次α衰变和10次β衰变 |
8. 如图所示,光滑水平面OB与足够长的粗糙斜面BC相接于B点,O端有一竖直墙面,一轻弹簧左端固定于竖直墙面,现用质量为m1的滑块压缩弹簧至D点,然后由静止释放,滑块脱离弹簧后经B点滑上斜面,上升到最大高度,并静止在斜面上,不计滑块在B点的机械能损失.若换用相同材料、相同粗糙程度、质量为m2(m2>m1) 的滑块压缩弹簧至同一点D后,重复上述过程,下列说法正确的是( )
如图所示,光滑水平面OB与足够长的粗糙斜面BC相接于B点,O端有一竖直墙面,一轻弹簧左端固定于竖直墙面,现用质量为m1的滑块压缩弹簧至D点,然后由静止释放,滑块脱离弹簧后经B点滑上斜面,上升到最大高度,并静止在斜面上,不计滑块在B点的机械能损失.若换用相同材料、相同粗糙程度、质量为m2(m2>m1) 的滑块压缩弹簧至同一点D后,重复上述过程,下列说法正确的是( )
 如图所示,光滑水平面OB与足够长的粗糙斜面BC相接于B点,O端有一竖直墙面,一轻弹簧左端固定于竖直墙面,现用质量为m1的滑块压缩弹簧至D点,然后由静止释放,滑块脱离弹簧后经B点滑上斜面,上升到最大高度,并静止在斜面上,不计滑块在B点的机械能损失.若换用相同材料、相同粗糙程度、质量为m2(m2>m1) 的滑块压缩弹簧至同一点D后,重复上述过程,下列说法正确的是( )
如图所示,光滑水平面OB与足够长的粗糙斜面BC相接于B点,O端有一竖直墙面,一轻弹簧左端固定于竖直墙面,现用质量为m1的滑块压缩弹簧至D点,然后由静止释放,滑块脱离弹簧后经B点滑上斜面,上升到最大高度,并静止在斜面上,不计滑块在B点的机械能损失.若换用相同材料、相同粗糙程度、质量为m2(m2>m1) 的滑块压缩弹簧至同一点D后,重复上述过程,下列说法正确的是( )| A. | 两滑块到达B点的速度相同 | |
| B. | 两滑块沿斜面上升的最大高度相同 | |
| C. | 两滑块上升到最高点的过程中克服重力做的功相同 | |
| D. | 两滑块上升到最高点的过程中机械能损失相同 |
 某同学测绘标有“4.8V,0.3A”字样的小灯泡的伏安特性曲线.为了使测量尽可能准确,除了导线和开关外,可供选择的仪器还有:
某同学测绘标有“4.8V,0.3A”字样的小灯泡的伏安特性曲线.为了使测量尽可能准确,除了导线和开关外,可供选择的仪器还有: 滑板极限运动场地如图,滑道AB水平,长为S,BC倾斜,CD为竖直平面内半径为R的圆弧,圆心0与C的连线与竖直方向夹角成a,D的切线方向竖直,一个质量(包括滑板)为m的运动员从A点静止出发,经B点飞出,恰好从C点的切线方向进入圆形滑道,再从D点竖直向上运动到达最高点E,已知E点相对圆弧滑道最低点的高度为E,重力加速度为g.则
滑板极限运动场地如图,滑道AB水平,长为S,BC倾斜,CD为竖直平面内半径为R的圆弧,圆心0与C的连线与竖直方向夹角成a,D的切线方向竖直,一个质量(包括滑板)为m的运动员从A点静止出发,经B点飞出,恰好从C点的切线方向进入圆形滑道,再从D点竖直向上运动到达最高点E,已知E点相对圆弧滑道最低点的高度为E,重力加速度为g.则