题目内容
在“利用单摆测重力加速度”的实验中:
(1)甲同学测得的重力加速度数值明显大于当地的重力加速度值,造成这一情况的可能原因是 ;
A.测量摆长时,把悬挂状态的摆线长当成摆长
B.测量周期时,当摆球通过平衡位置时启动秒表并记为第1次,此后摆球第50次通过平衡位置时制动秒表,读出经历的时间为t,并由计算式T=
求得周期
C.开始摆动时振幅过小
D.所用摆球的质量过大
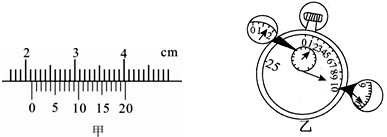
(2)乙同学先用米尺测得摆线长为97.43cm,用卡尺测得摆球直径如图甲所示为 cm,然后用秒表记录单摆完成全振动50次所用的时间,从图乙可读出时间为 s,当地的重力加速度g= m/s2.(重力加速度的计算结果保留三位有效数字)
(3)实验中,如果摆球密度不均匀,无法确定重心位置,丙同学设计了一个巧妙的方法而不用测量摆球的半径.具体作法如下:
①第一次悬线长为L1时,测得振动周期为T1;
②第二次增大悬线长为L2时,测得振动周期为T2;
③根据单摆周期公式可求得重力加速度为g= .(用题给符号表示)
(1)甲同学测得的重力加速度数值明显大于当地的重力加速度值,造成这一情况的可能原因是
A.测量摆长时,把悬挂状态的摆线长当成摆长
B.测量周期时,当摆球通过平衡位置时启动秒表并记为第1次,此后摆球第50次通过平衡位置时制动秒表,读出经历的时间为t,并由计算式T=
| t | 25 |
C.开始摆动时振幅过小
D.所用摆球的质量过大
(2)乙同学先用米尺测得摆线长为97.43cm,用卡尺测得摆球直径如图甲所示为
(3)实验中,如果摆球密度不均匀,无法确定重心位置,丙同学设计了一个巧妙的方法而不用测量摆球的半径.具体作法如下:
①第一次悬线长为L1时,测得振动周期为T1;
②第二次增大悬线长为L2时,测得振动周期为T2;
③根据单摆周期公式可求得重力加速度为g=

分析:由单摆周期公式,求出重力加速度的表达式,根据重力加速度的表达式,分析重力加速度测量值偏大的原因.
游标卡尺的读数:先读主尺,再加上游标尺(格数乘以分度分之一,格数找对齐的一个不估读),
秒表的读数:先读内圈,读数时只读整数,小数由外圈读出,读外圈时,指针是准确的,不用估读,代入g的表达式可求解;
设摆球的重心到线与球结点的距离为r,根据单摆周期的公式分别列出方程,求解重力加速度.
游标卡尺的读数:先读主尺,再加上游标尺(格数乘以分度分之一,格数找对齐的一个不估读),
秒表的读数:先读内圈,读数时只读整数,小数由外圈读出,读外圈时,指针是准确的,不用估读,代入g的表达式可求解;
设摆球的重心到线与球结点的距离为r,根据单摆周期的公式分别列出方程,求解重力加速度.
解答:解:(1)由单摆周期公式T=2π
,可知重力加速度:g=
A、由g=
可知,当l偏小会才会引起测量值小,故A错误
B、由g=
可知,当T偏小会引起测量值偏大.故B正确.
C、重力加速度的测量值与振幅无关,振幅偏小,不影响测量结果,故C错误;
D、g的值与摆球的质量无关,故D错误
故选:B
(2)直径:主尺:2.1cm,游标尺对齐格数:5个格,读数:5×
mm=0.25mm=0.025cm
所以直径为:2.1+0.025=2.125cm
秒表读数:内圈:1.5分钟=90s,外圈:9.8s,所以读数为:99.8s
由g=
,L=97.43+
=98.49cm,T=
s=1.996s
代入解得:g=9.75m/s2
(3)设摆球的重心到线与球结点的距离为r,根据单摆周期的公式:T=2π
故:T1=2π
T2=2π
联立两式解得:g=
故答案为:(1)B;(2)2.125,99.8,9.75;(3)
|
| 4π2L |
| T2 |
A、由g=
| 4π2L |
| T2 |
B、由g=
| 4π2L |
| T2 |
C、重力加速度的测量值与振幅无关,振幅偏小,不影响测量结果,故C错误;
D、g的值与摆球的质量无关,故D错误
故选:B
(2)直径:主尺:2.1cm,游标尺对齐格数:5个格,读数:5×
| 1 |
| 20 |
所以直径为:2.1+0.025=2.125cm
秒表读数:内圈:1.5分钟=90s,外圈:9.8s,所以读数为:99.8s
由g=
| 4π2L |
| T2 |
| 2.125 |
| 2 |
| 99.8 |
| 50 |
代入解得:g=9.75m/s2
(3)设摆球的重心到线与球结点的距离为r,根据单摆周期的公式:T=2π
|
故:T1=2π
|
T2=2π
|
联立两式解得:g=
| 4π2(L1-L2) | ||||
|
故答案为:(1)B;(2)2.125,99.8,9.75;(3)
| 4π2(L1-L2) | ||||
|
点评:解决本题的关键掌握单摆的周期公式,知道测量重力加速度的原理

练习册系列答案
相关题目

