题目内容
【题目】如图所示,质量为M的木板C放在水平地面上,固定在C上的竖直轻杆的顶端分别用细绳a和b连接小球A和小球B,小球A、B的质量分别为mA和mB,当与水平方向成30°角的力F作用在小球B上时,A、B、C刚好相对静止一起向右匀速运动,且此时绳a、b与竖直方向的夹角分别为30°和60°,则下列判断正确的是( )
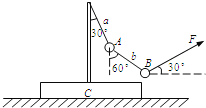
A. 力F的大小为mBg
B. 地面对C的支持力等于(M+mA+mB)g
C. 地面对C的摩擦力大小为![]()
D. mA=mB
【答案】ACD
【解析】以B为研究对象,分析受力,水平方向受力平衡,则有:Fcos30°=Tbcos30°,得:Tb=F
竖直方向受力平衡,则:Fsin30°+Tbsin30°=mBg得:F=mBg,故A正确;以ABC整体为研究对象受力分析,竖直方向:N+Fsin30°=(M+mA+mB)g, 可见N小于(M+mA+mB)g,故B错误;以ABC整体为研究对象受力分析,水平方向:f=Fcos30°=mBgcos30°=![]() mBg,故C正确;以A为研究对象受力分析,竖直方向:mAg+Tbsin30°=Tasin60°;水平方向:Tasin30°=Tbsin60°;联立得:mA=mB,故D正确;故选ACD.
mBg,故C正确;以A为研究对象受力分析,竖直方向:mAg+Tbsin30°=Tasin60°;水平方向:Tasin30°=Tbsin60°;联立得:mA=mB,故D正确;故选ACD.
点睛:本题考查受力分析以及平衡条件的应用,关键是灵活的选择研究对象,采用隔离法和整体法结合比较简便.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目