题目内容
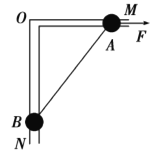
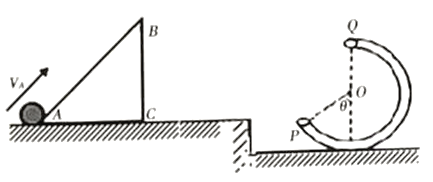
【题目】如图所示固定光滑斜面ABC,其中AC= BC=2.5m,质量为m= 1kg的小球(可视为质点),以10m/s的初速度从底端A冲上斜面,恰好沿P点切线进入口径很小的光滑圆管轨道中,圆心为O,轨道半径R= 1m,且OP与竖直方向的夹角为![]() ,Q点为轨道最高点(不计空气阻力,取g= 10m/s2).求:
,Q点为轨道最高点(不计空气阻力,取g= 10m/s2).求:
(1)小球从B点抛出后在空中运动到最高点时的速度;
(2)小球从A点运动到P点所用的时间;
(3)小球在Q点对圆弧轨道的作用力.
【答案】(1)5m/s (2)1.78s (3)60N
【解析】
(1)设AB的长为s,小球体从A到B过程中,由动能定理得:
![]()
解得:
![]()
小球到B点抛出后做斜抛运动,在B点将速度沿水平方向和竖直方向分解,得
![]()
小球斜抛到最高点后只保留水平方向的速度,所以
v最高点= 5m/s
(2)小球从A运动到B,设时间为t1,加速度为a,则
![]()
![]()
设小球从B点斜抛到最高点的过程中所用的时间为t2则
![]()
小球运动到P点时将速度分解:
![]()
设小球从最高点运动到P点的时间为t3
![]()
得
![]()
所以小球从A点运动到P点所用的总时间:
 ;
;
(3)小球从P到Q过程中,由动能定理得
![]()
解得:
![]()
在Q点,当小球对圆弧轨道的作用力为零时,由重力提供向心力得:
![]()
解得:
![]()
因为![]() ,所以在Q点圆轨道对小球的作用力FN方向竖直向下.由牛顿第二定律得:
,所以在Q点圆轨道对小球的作用力FN方向竖直向下.由牛顿第二定律得:
![]()
解得:
FN=60N
由牛顿第三定律知:在Q点小球对圆弧轨道的作用力方向竖直向上,大小为60N.

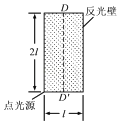
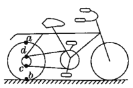
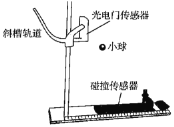
【题目】如图所示,研究平抛运动规律的实验装置放置在水平桌面上,利用光电门传感器和碰撞传感器可测得小球的水平初速度和飞行时间,底板上的标尺可以测得水平位移。保持水平槽口距底板高度![]() 不变。改变小球在斜槽导轨上下滑的起始位置,测出小球做平抛运动的初速度、飞行时间t和水平位移d,记录在表中。
不变。改变小球在斜槽导轨上下滑的起始位置,测出小球做平抛运动的初速度、飞行时间t和水平位移d,记录在表中。
| 0.741 | 1.034 | 1.318 | 1.584 |
t/ms | 292.7 | 293.0 | 292.8 | 292.9 |
d/cm | 21.7 | 30.3 | 38.6 | 46.4 |
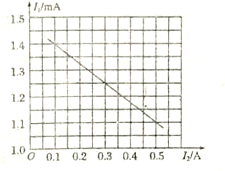
(1)由表中数据可知,在h一定时,小球水平位移d与其初速度![]() 成_______关系。
成_______关系。
(2)一位同学计算出小球飞行时间的理论值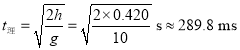 ,发现理论值与测量值之差约为3 ms。经检查,实验及测量无误,其原因是__________。
,发现理论值与测量值之差约为3 ms。经检查,实验及测量无误,其原因是__________。
(3)另一位同学分析并纠正了上述偏差后,重新做了这个实验,竟发现测量值![]() 依然大于自己得到的理论值
依然大于自己得到的理论值![]() ,但二者之差在3~7 ms,且初速度越大差值越小。对实验装置的安装进行检查,确认斜槽槽口与底座均水平,则导致偏差的原因是__________。
,但二者之差在3~7 ms,且初速度越大差值越小。对实验装置的安装进行检查,确认斜槽槽口与底座均水平,则导致偏差的原因是__________。