题目内容
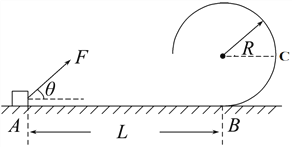
【题目】如图所示，在粗糙水平面上竖直固定半径为R＝10 cm的光滑圆轨道，质量为m＝4 kg的物块静止放在粗糙水平面上的A处，物块与水平面间的动摩擦因数μ＝0.4，A与B的间距L＝0.76 m，现对物块施加大小为F=25N，方向与水平方向成
370角的恒定拉力，使其沿粗糙水平面做直线运动，到达B处将拉力F撤去，物块沿竖直光滑圆轨道运动，重力加速度g取10 m/s2， 
，物块可视为质点．求：
（1）物块到达与圆心等高处C处时的动能；
（2）试判断物块是否可以通过圆轨道最高点；若不能，物块离开圆轨道时距B点的高度是多少？（提示：在圆周运动过程中的任一点，质点所受的向心力与其速度的关系为
）
【答案】（1）3.6J；（2）16cm；
【解析】解：（1）从A点到B点的过程中
解得： 
（2）若物块恰好通过最高点，则在最高点有
从B点到最高点的过程中： 
解得： 
所以不能到达最高点
设离开圆轨道的点C和圆心连线与水平方向夹角为
，则从B点到C点的过程中，根据机械能守恒：
在C点： 
C距B点的高度
解得：H=16cm
综上所述本题答案是：（1）3.6J；（2）16cm
练习册系列答案
相关题目
