题目内容
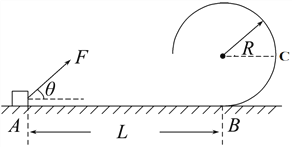
【题目】如图所示，平台上的小球从A点水平抛出，恰能无碰撞地进入光滑的BC斜面，经C点进入光滑平面CD时速率不变，最后进入悬挂在O点并与水平面等高的弧形轻质筐内．已知小球质量为m，A、B两点高度差h，BC斜面高2h，倾角α=45°，悬挂弧筐的轻绳长为3h，小球看成质点，弧形轻质筐的大小远小于悬线长度，重力加速度为g，试求：
（1）B点与抛出点A的水平距离x；
（2）小球运动至C点的速度
大小；
（3）小球进入轻质筐后瞬间，绳上拉力F的大小．
【答案】（1）
（2）
（3）
【解析】试题分析：（1）小球从A到B做平抛运动，小球恰好与无碰撞地进入光滑的BC斜面，速度沿BC面向下，可得到两个方向的分速度关系．从水平方向和竖直方向运用平抛运动的规律分析解决问题，
（2）运用动能定理可求解小球到达C点的速度，
（3）小球进入轻质筐后瞬间，进行受力分析，并运用牛顿第二定律求解。
解：(1)小球至B点时速度方向与水平方向夹角为45°，设小球抛出的初速度为v0，A点至B点时间为t．则得： 
，得
，又
得： 
，得水平距离： 
；
(2) 设小球至B点时速度为vB，在斜面上运动的加速度为a，
a=gsin45°，
由以上各式解得： 
；
(3) 小球进入轻筐后做圆周运动，由牛顿第二定律得： 
解得小球所受拉力： 
。
练习册系列答案
名校课堂系列答案
相关题目
