Question

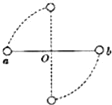
【题目】如图所示，三角形传送带以1 m/s的速度逆时针匀速转动，两边的传送带长都是2 m，且与水平方向的夹角均为37°.现有两个物块A、B从传送带顶端都以大小为v0＝1 m/s的初速度沿传送带下滑，物块A、B与传送带间的动摩擦因数都是0.5，取g＝10 m/s2，sin 37°＝0.6，cos 37°＝0.8.下列说法正确的是( )

A. 物块A、B同时到达传送带底端

B. 传送带对物块A做正功，对B做负功

C. 物块A、B在传送带上的划痕长度之比为1∶3

D. 滑动摩擦力对物块A与传送带做的功之和与滑动摩擦力对物块B与传送带做的功之和一样大

Answer 1

【答案】AC

【解析】在平行传送带的方向上，由于mgsin 37°>μmgcos 37°，物块A、B均沿传送带加速向下滑动，传送带对物块A、B的摩擦力都沿传送带向上，加速度大小均为a＝＝2 m/s2，初速度大小v0相同，又因为两边的传送带长度相同，根据x＝v0t＋at2可知两者的运动时间均为t＝1 s，即两者同时到达底端，选项A正确．滑动摩擦力与位移方向均相反，摩擦力均做负功，选项B错误；B到达传送带底端时的速度大小vB＝v0＋at＝3 m/s，传送带在1 s内的路程x＝vt＝1 m，A与传送带是同向运动的，A的划痕长度为A与传送带相对位移的大小，即2 m－1 m＝1 m．B与传送带是反向运动的，B的划痕长度为B与传送带相对位移的大小，即2 m＋1 m＝3 m，即物块A、B在传送带上的划痕长度之比为1∶3，选项C正确；物块A的位移大小为2 m，A受到的滑动摩擦力与位移方向相反而做负功，A受到的滑动摩擦力做的功Wf1＝－f×(2 m)，传送带的位移大小为1 m，传送带受到的滑动摩擦力与位移方向相同而做正功，滑动摩擦力对传送带做的功Wf2＝f×(1 m)，滑动摩擦力对A做的功与对传送带做的功之和Wf＝Wf1＋Wf2＝－f×(1 m)，物块B的位移大小为2 m，B受到的滑动摩擦力与位移方向相反而做负功，B受到的滑动摩擦力做的功W′f1＝－f×(2 m)，传送带的位移大小为1 m，传送带受到的滑动摩擦力与位移方向相反而做负功，滑动摩擦力对传送带做的功W′f2＝－f×(1 m)，滑动摩擦力对B做的功与对传送带做的功之和W′f＝W′f1＋W′f2＝－f×(3 m)，即Wf≠W′f，选项D错误．故选AC.