题目内容
(8分)如图所示,质量m=0.05kg的小球用一根长度L=0.8m的细绳悬挂在天花板的O点,悬线竖直时小球位于C点。若保持细线张紧,将小球拉到位置A,然后将小球由静止释放。已知OA与竖直方向的夹角θ=37°,忽略空气阻力,重力加速度g取10m/s2。(已知sin37°=0.6,cos37°=0.8)。求: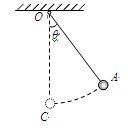
(1)小球经过C点时的动能;
(2)小球运动到C点时受到细绳的拉力大小;
(3)若在O和C之间某位置D有一水平钉子,使得细绳恰好能拉着小球绕D点做圆周运动。求D点与天花板的距离。
(1)0.08J;(2)0.7N;(3)0.736m。
解析试题解析:(1)小球由A点到C点,利用机械能守恒可得:mg(L-Lcosθ)= mv2,
mv2,
故小球经过C点时的动能Ek= mg(L-Lcosθ)=0.05×10×0.8(1-0.8)=0.08J;
(2)在C点时,应用牛顿第二定律得:F-mg=m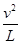 ,
,
故小球运动到C点时受到细绳的拉力大小F=0.7N;
(3)设D点与天花板的距离为R,小球做圆周运动到最上端的速度为v′,
则根据机械能守恒定律得:mg(L-Lcosθ)= mg×2(L-R)+  mv′2,
mv′2,
再根据牛顿第二定律得:mg=m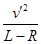 ,
,
联立以上两式,解之得R=0.92L=0.736m.
考点:机械能守恒,圆周运动,牛顿第二定律。

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
质量为m的汽车在平直公路上行驶,阻力f保持不变。当汽车的速度为v、加速度为a时,发动机的实际功率为
| A.fv | B.mav | C.(ma+f)v | D.(ma-f)v |

 的
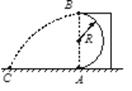
的 光滑圆弧形固定轨道接触(但不粘连),木板的右端到竖直墙的距离为s;另一质量为2m的小滑块从轨道的最高点由静止开始下滑,从圆弧的最低点A滑上木板。设长木板每次与竖直墙的碰撞时间极短且无机械能损失。已知滑块与长木板间的动摩擦因数为μ。试求:
光滑圆弧形固定轨道接触(但不粘连),木板的右端到竖直墙的距离为s;另一质量为2m的小滑块从轨道的最高点由静止开始下滑,从圆弧的最低点A滑上木板。设长木板每次与竖直墙的碰撞时间极短且无机械能损失。已知滑块与长木板间的动摩擦因数为μ。试求:
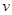 与s的关系;
与s的关系;