题目内容
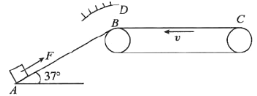
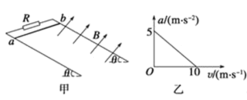
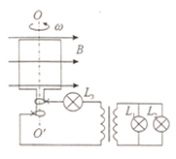
【题目】如图所示,面积为S、匝数为N的矩形线框在磁感应强度为B的匀强磁场中,绕垂直于磁感线的轴OO′匀速转动,通过滑环向理想变压器供电,灯泡L1、L2、L3均正常发光。已知L1、L2、L3的额定功率均为P,额定电流均为I,线框及导线电阻不计,则( )
A. 理想变压器原副线圈的匝数比为1:2
B. 图示位置时穿过线框的磁通量变化率为零
C. 若灯L1烧断,灯泡L3将变暗
D. 线框转动的角速度为![]()
【答案】C
【解析】
A.灯泡L1、L2、L3均正常发光,则原线圈电流强度I1=I,副线圈电流强度I2=2I,所以![]() ,故A错误;
,故A错误;
B.图示位置时,线框切割速度最大,故穿过线框的磁通量变化率最大,故B错误;
C.开始时若设每盏灯的额定电压为U,则变压器初级电压为2U,线圈输入电压为3U;若L1灯烧断,设L3的电压变为U1,则变压器输入电压为3U-U1,次级电压变为![]() ,次级电流为:
,次级电流为:![]() ,则初级电流为
,则初级电流为![]() ,则L3两端电压为
,则L3两端电压为![]() ,解得U1=0.6U,则灯泡L3两端电压减小,亮度变暗,故C正确;
,解得U1=0.6U,则灯泡L3两端电压减小,亮度变暗,故C正确;
D.线框的输出功率为3P,电流为I,则线框产生的感应电动势为![]() ,根据Em=NBSω,
,根据Em=NBSω,![]() ,联立解得:
,联立解得:![]() ,故D错误。
,故D错误。

 名校课堂系列答案
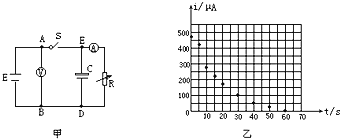
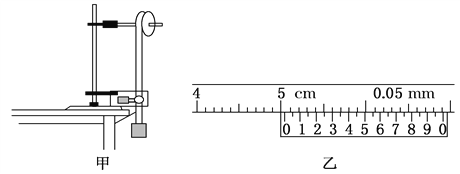
名校课堂系列答案【题目】如图甲为研究“转动动能与角速度关系”的实验装置示意图,现有的器材为:固定在竖直平面内的转盘(转轴水平)、带铁夹的铁架台、电磁打点计时器(接交流电的频率为50 Hz)、纸带、重锤、游标卡尺、天平.回答下列问题 :
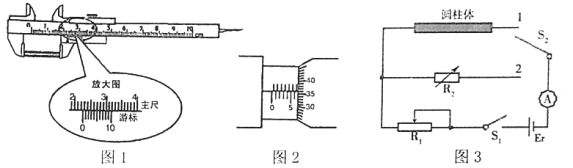
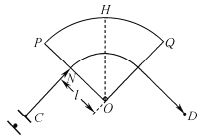
(1)如图乙所示,用20分度的游标卡尺测得圆盘的直径d为________ cm;
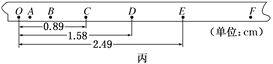
(2)将悬挂铁锤的纸带穿过打点计时器后,绕在转盘边缘上,纸带一端固定在转盘上,使得转盘与纸带不打滑,设纸带厚度不计,接通电源,释放重锤,打点计时器打出的纸带如图丙所示,O、A、B、C…各点为连续打出的点迹,则由图丙中数据可得,打下点迹D时,圆盘转动的角速度为ωD=____________ rad/s(保留三位有效数字);
(3)下表为各点对应的转动动能Ek和角速度ω值,请你猜想转动动能Ek和角速度ω满足的关系式为Ek=____________(须填写定量表达式).
计数点 | A | B | C | … | E |
转动动能Ek(J) | 0.001 0 | 0.003 9 | 0.008 9 | … | 0.024 |
角速度ω(rad/s) | 4.0 | 7.9 | 11.9 | … | 19.7 |