题目内容
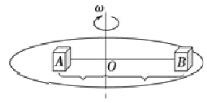
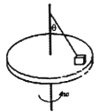
【题目】如图所示,水平转台上有一个质量m为的物块,用长为L的细绳将物块连接在转轴上,细线与竖直转轴的夹角为![]() 角,此时绳中张力为零,物块与转台间动摩擦因数为
角,此时绳中张力为零,物块与转台间动摩擦因数为![]() ,最大静摩擦力等于滑动摩擦力,物块随转台由静止开始逐渐加速转动,则下列说法中正确的是( )
,最大静摩擦力等于滑动摩擦力,物块随转台由静止开始逐渐加速转动,则下列说法中正确的是( )
A. 物块离开转台之前所受摩擦力始终指向转轴
B. 当转台角速度![]() 时,物块将离开转台
时,物块将离开转台
C. 当物块的动能为![]() 时,物块对转台的压力恰好为零
时,物块对转台的压力恰好为零
D. 当转台的角速度![]() 时,随着角速度的增加,细线与转轴的夹角增大
时,随着角速度的增加,细线与转轴的夹角增大
【答案】CD
【解析】
对物块进行受力分析,由牛顿第二定律求得绳中出现拉力和转台对物块支持力为零时物块的速度。
A、在物块随转台由静止开始缓慢加速转动的过程中,物块要受到沿圆弧切线方向的摩擦力的分力使物块加速,故A错误。
B、设当转台的角速度比较小时,物块只受重力、支持力和摩擦力,当细绳恰好要产生拉力时:![]() mg=m
mg=m![]() L
L![]() ,解得
,解得![]() =
=![]() ,随着角速度的增大,细绳上的拉力增大,当物块恰好要离开转台时,物块受的重力和细绳的拉力的合力充当向心力有:mg
,随着角速度的增大,细绳上的拉力增大,当物块恰好要离开转台时,物块受的重力和细绳的拉力的合力充当向心力有:mg![]() =m
=m![]() L
L![]() ,解得
,解得![]() =
=![]() ,此时物块的动能EK=
,此时物块的动能EK=![]() m
m![]() =
=![]() ,故B错误,C正确。
,故B错误,C正确。
D、当转台的角速度![]() 时,物块离开转台后,随着角速度的增加,细线与转轴的夹角增大,D正确。
时,物块离开转台后,随着角速度的增加,细线与转轴的夹角增大,D正确。
故选:C、D

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目